《编译原理实验》
实验报告
| 题 目 | : | 第二次实验 自上而下语法分析 |
| 姓 名 | : | 高星杰 |
| 学 号 | : | 2021307220712 |
| 专 业 | : | 计算机科学与技术 |
| 上课时间 | : | 2024-春 |
| 授课教师 | : | 刘善梅 |
2024 年 4月 11 日
[TOC]
编译原理 第二次实验 自上而下语法分析
实验目的
- 能采用LL(1)分析法对一个算术表达式(a+15)*b做自上而下的语法分析;
- 可自行设计一个文法,能识别类似(a+15)*b句子的语言;
- 也可基于PL/0语言的文法(完整文法参见本文档最后的附录)来做,若基于PL/0语言文法,需重点关注以下几条文法的EBNF,若不习惯看文法的巴科斯范式EBNF,可先将文法改写成常规的产生式形式P75。
- 通过设计、编制、调试一个具体的文法分析程序,深入理解LL(1)预测分析法的基本分析原理.
- 理解FIRST集、FOLLOW集的构造方法并对其加以实现,构造LL(1)预测分析表并利用分析表对语句、文法进行分析。
- 加深对的语法分析的理解
PL/0 语言文法的EBNF
<程序>::=<分程序>. <分程序> ::=\[<常量说明>]\[<变量说明>][<过程说明>]<语句> <常量说明> ::=CONST<常量定义>{,<常量定义>}; <常量定义> ::=<标识符>=<无符号整数> <无符号整数> ::= <数字>{<数字>} <变量说明> ::=VAR <标识符>{, <标识符>}; <标识符> ::=<字母>{<字母>|<数字>} <过程说明> ::=<过程首部><分程序>{; <过程说明> }; <过程首部> ::=PROCEDURE <标识符>; <语句> ::=<赋值语句>|<条件语句>|<当循环语句>|<过程调用语句> |<复合语句>|<读语句><写语句>|<空> <赋值语句> ::=<标识符>:=<表达式> <复合语句> ::=BEGIN <语句> {;<语句> }END <条件语句> ::= <表达式> <关系运算符> <表达式> |ODD<表达式> <表达式> ::= [+|-]<项>{<加法运算符> <项>} <项> ::= <因子>{<乘法运算符> <因子>} <因子> ::= <标识符>|<无符号整数>| ‘(’<表达式>‘)’ <加法运算符> ::= +|- <乘法运算符> ::= *|/ <关系运算符> ::= =|#|<|<=|>|>= <条件语句> ::= IF <条件> THEN <语句> <过程调用语句> ::= CALL 标识符 <当循环语句> ::= WHILE <条件> DO <语句> <读语句> ::= READ‘(’<标识符>{,<标识符>}‘)’ <写语句> ::= WRITE‘(’<表达式>{,<表达式>}‘)’ <字母> ::= a|b|…|X|Y|Z <数字> ::= 0|1|…|8|9 **PL/0 语言文法的产生式** ```gfm E->AXF|XF F->AXF|@ X->YZ Z->CYZ|@ Y->b|z|(E) A->+|- C->*|/ ``` @ 代表 空
实验任务
采用预测分析法实现自上而下的语法分析;采用递归下降分析法得到的结果不得分。若自行设计的文法含左递归,要写程序消除左递归。
编程基础扎实的同学,强烈建议用程序分别求解first集和follow集,并用程序实现预测分析表;
编程基础非常薄弱的同学,可以人工求解first集和follow集,人工设计好预测分析表,然后直接在程序中给出手工设计好的预测分析表。
编程基础尚可的同学,可根据自身情况编程求解 first集、follow集和预测分析表这三个部分的某些部分。(书上都有算法,建议同学们尽量用程序实现)
我实现了用程序分别求解first集和follow集,并用程序实现预测分析表;
实验完成程度
| 实现的内容 | 实现的方式 |
|---|---|
| 求解First集 | 程序实现 |
| 求解Follow集 | 程序实现 |
| 求解预测分析表 | 程序实现 |
| 判断是否是LL(1)文法 | 程序实现 |
| 使用预测分析表进行分析 | 程序实现 |
| 是否仅支持PL/0文法 | 否、可以输出其他文法和句子进行判断 |
设计思想
LL(1)语法分析器的实现相比递归下降而言复杂了很多,但概括起来程序的实现总共需要如下几步:
- 构造非终结符的First集
- 构造非终结符的Follow集
- 根据First集和Follow集构造LL(1)分析表
- 判断是否是LL(1)文法
- 根据分析表构造分析栈逐个匹配

1. 数据结构设计
- 字符与编号映射:使用
map数据结构将字符映射到编号(gtnum)以及编号映射到字符(gtchar),方便快速查找。 - 文法集合:使用
vector<string>存储文法产生式集合。 - 预测分析表:使用二维数组
table存储预测分析表。 - First、Follow、Select 集合:使用字符串数组分别存储每个非终结符的First、Follow、Select集合。
2. 初始化与输入读取
- 读取文法规则:通过字符串流(
stringstream)读取预定义的文法规则、终结符和非终结符。将这些符号映射到唯一编号,并存储在相应的数据结构中。
3. First集合计算
- 递归计算:对每个终结符,其First集合是其本身。对每个非终结符,递归计算其First集合,通过合并产生式右部各符号的First集合来获取。
- 合并与判断空字:使用
Union函数合并多个集合,并判断产生式能否推出空字。
4. Follow集合计算
- 初始化Follow集合:对开始符号,其Follow集合初始化为包含终结符
#。 - 递归获取:遍历所有产生式,考虑右部符号的后续符号的First集合,根据能否推出空字来更新Follow集合。
5. Select集合计算
- 直接推出空字:对于右部能直接推出空字的产生式,Select集合为左部符号的Follow集合。
- 合并First集合:对其他产生式,Select集合为右部第一个符号的First集合,如果多个符号均可推出空字,则继续考虑后续符号的First集合,直到无法推出空字为止。
6. 预测分析表生成
- 构建表项:根据Select集合构建预测分析表。对于能直接推出空字的产生式,使用Follow集合填表。对于其他产生式,使用First集合填表。
7. LL(1)文法检查
- 交集判断:定义
intersection函数检查两个集合是否有交集。遍历所有产生式,检查同一个非终结符的不同产生式的Select集合是否有交集。 - 结果输出:如果有交集,则输出产生冲突的Select集合,并判定该文法不是LL(1)文法;如果所有Select集合均无交集,则判定该文法是LL(1)文法。
8. 句子合法性分析
- 分析过程:定义一个
analyze函数,通过栈模拟分析过程。初始化栈并推入起始符号和终结符。逐步从输入串中读取符号,并根据预测分析表中的指引,逐步匹配和推导输入串。 - 结果判定:如果输入串能够完全匹配并使栈空,则输入串符合文法;否则,不符合文法。
算法流程
算法流程图
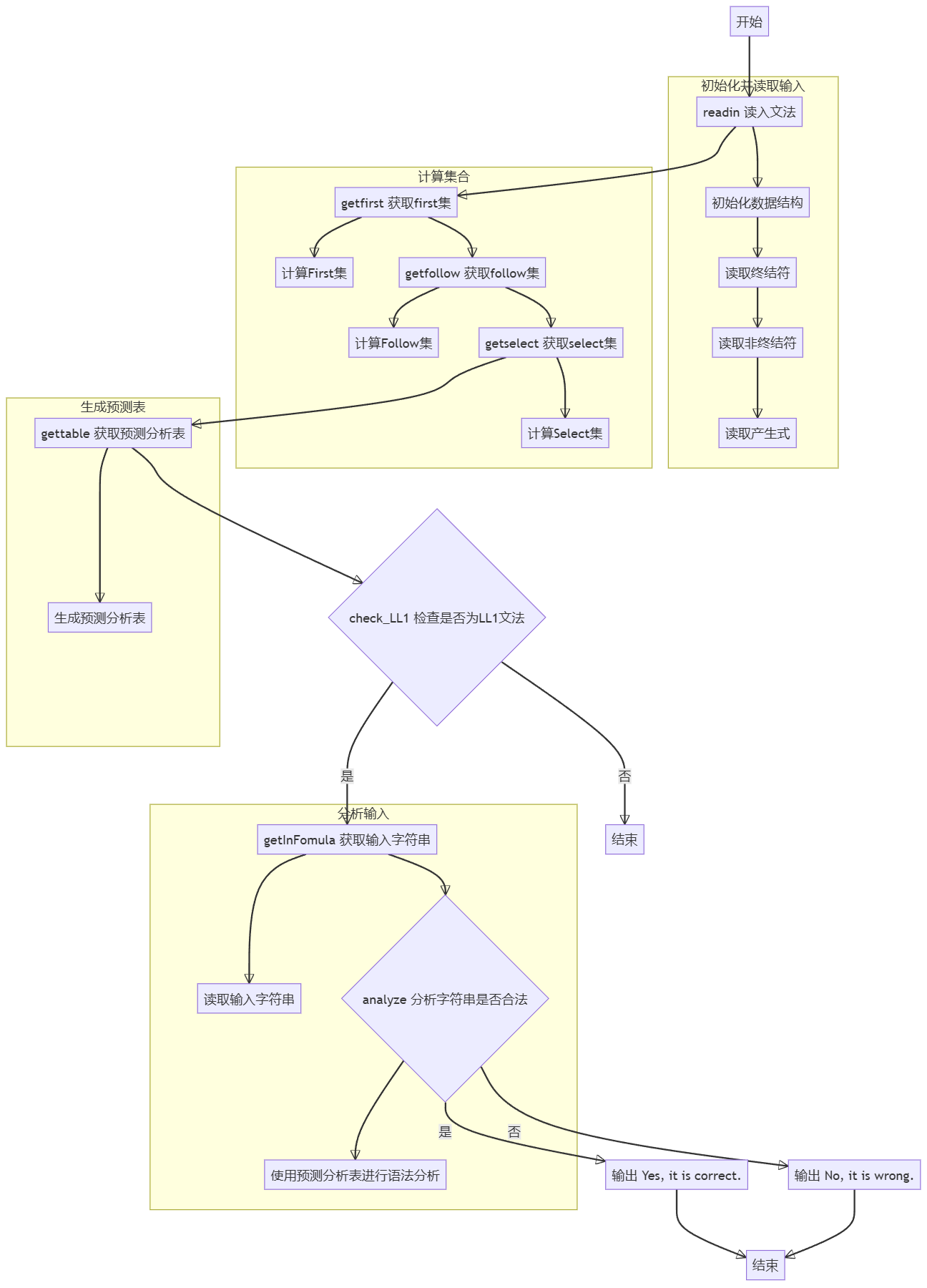
本次实验是先实现了对各种文法的一般算法,然后为了让itc通过,对itc 的输入格式进行了适配的,所以本质上还是可以通过输入文法来进行LL1分析的。
1 获取First集
- 初始化:
- 对于每个终结符,First集是其本身。
- 初始化所有非终结符的First集为空集。
- 处理每个产生式:
- 对于每个产生式$A \rightarrow \alpha$,我们从左到右处理’产生式中的每个符号。
- 如果是终结符,直接加入 A 的First集。
- 如果是非终结符,将该非终结符的First集(去掉空字)加入 A 的First集。
- 如果该非终结符可以推出空字($\epsilon$),继续处理下一个符号。
- 如果所有符号都可以推出空字,则将空字加入 A 的First集。
2 获取Follow集
- 初始化:
- 对于开始符号,将结束符号(#)加入其Follow集。
- 处理每个产生式:
- 对于每个产生式$ A \rightarrow \alpha B \beta$,将 β\betaβ 的First集(去掉空字)加入 B 的Follow集。
- 如果 $\beta$ 可以推出空字,将 A 的Follow集加入 B 的Follow集。
- 迭代处理:
- 多次扫描所有产生式,直到所有Follow集都不再变化。
3 获取Select集
- 处理每个产生式:
- 对于每个产生式$ A \rightarrow \alpha$:
- 如果$ \alpha$可以直接推出空字,将 A 的Follow集加入该产生式的Select集。
- 否则,将$ \alpha$的First集加入该产生式的Select集。、
- 对于每个产生式$ A \rightarrow \alpha$:
4 检查LL(1)文法:
- 遍历所有产生式,检查同一个非终结符对应的不同产生式的Select集是否有交集。
- 如果有交集,说明该文法不是LL(1)文法,并输出产生冲突的Select集。
- 如果没有交集,说明该文法是LL(1)文法。
5 获取预测分析表
- 初始化:
- 初始化预测分析表为-1,表示为空。
- 处理每个产生式:
- 对于每个产生式 $A \rightarrow \alpha$
- 对于该产生式的Select集中的每个终结符,将对应表项设置为该产生式的编号。
- 对于每个产生式 $A \rightarrow \alpha$
6 根据预测分析表构造分析栈并逐个匹配输入字符串
- 初始化分析栈:
- 分析栈初始状态为
#和开始符号。 - 输入串在末尾加上结束符号
#。
- 分析栈初始状态为
- 逐步匹配:
- 栈顶符号与当前输入符号进行比较。
- 如果栈顶符号与当前输入符号相同,匹配成功,弹出栈顶符号并推进输入符号。
- 如果栈顶符号是非终结符,查预测分析表,根据表中的产生式进行展开,即用产生式右部替换栈顶符号。
- 如果栈顶符号是终结符且与当前输入符号不同,或者预测分析表中无对应产生式,解析失败。
- 当栈为空且输入符号也匹配完毕时,解析成功。
具体流程实现
1. 初始化与读取输入
void readin()
{
stringstream datascin(datas);
stringstream endcin(endchar);
stringstream noendcin(noendchar);
memset(table, -1, sizeof(table));
gtnum['#'] = 0;
gtchar[0] = '#';
char x;
do
{
endcin >> x;
gtnum[x] = ++num;
gtchar[num] = x;
} while (endcin.peek() != '\n');
numvt = ++num;
gtnum['@'] = numvt; // 空,用@表示
gtchar[num] = ('@');
do
{
noendcin >> x;
gtnum[x] = ++num;
gtchar[num] = x;
} while (noendcin.peek() != '\n');
string pro;
while (datascin >> pro && pro != "end")
{
string ss;
ss += pro[0];
for (int i = 3; i < pro.size(); i++)
{
if (pro[i] == '|')
{
proce.push_back(ss);
ss.clear();
ss += pro[0];
}
else
{
ss += pro[i];
}
}
proce.push_back(ss);
}
}
2. 生成First集
void getfirst()
{
for (int i = 1; i <= numvt; i++)
{
first[i] += ('0' + i);
}
for (int j = 0; j < proce.size(); j++)
{
int k = 0;
int has_0 = 0;
do
{
has_0 = 0;
k++;
if (k == proce[j].size())
{
first[gtnum[proce[j][0]]] += ('0' + numvt);
break;
}
Union(first[gtnum[proce[j][0]]], get_first(gtnum[proce[j][k]], has_0));
} while (has_0);
}
}
3. 生成Follow集
cpp复制代码void getfollow()
{
Union(follow[gtnum[proce[0][0]]], "0");
for (int j = 0; j < proce.size(); j++)
{
for (int jj = 1; jj < proce[j].size(); jj++)
{
if (gtnum[proce[j][jj]] <= numvt)
continue;
int k = jj;
int has_0;
do
{
has_0 = 0;
k++;
if (k == proce[j].size())
{
Union(follow[gtnum[proce[j][jj]]], follow[gtnum[proce[j][0]]]);
break;
}
Union(follow[gtnum[proce[j][jj]]], get_first(gtnum[proce[j][k]], has_0));
} while (has_0);
}
}
}
4. 生成Select集
void getselect()
{
for (int i = 0; i < proce.size(); i++)
{
if (proce[i][1] == '@')
{
selects[i] = follow[gtnum[proce[i][0]]];
continue;
}
if (gtnum[proce[i][1]] < numvt)
{
selects[i] = first[gtnum[proce[i][1]]];
continue;
}
int flag1 = 0;
for (int j = 1; j < proce[i].size(); j++)
{
string tepf = first[gtnum[proce[i][j]]];
int flag2 = 1;
for (int k = 0; k < tepf.size(); k++)
{
if (tepf[k] == ('0' + numvt))
{
flag2 = 0;
break;
}
}
if (flag2)
{
Union(selects[i], tepf);
flag1 = 0;
break;
}
int has_0 = 0;
Union(selects[i], get_first(gtnum[proce[i][j]], has_0));
flag1 = 1;
}
if (flag1)
{
Union(selects[i], follow[gtnum[proce[i][0]]]);
}
}
}
5. 检查LL(1)文法条件
bool intersection(string a, string b)
{
for (int i = 0; i < a.size(); i++)
{
for (int j = 0; j < b.size(); j++)
{
if (a[i] == b[j])
return 1;
}
}
return 0;
}
bool check_LL1()
{
for (int i = 0; i < proce.size(); i++)
{
for (int j = i + 1; j < proce.size(); j++)
{
if (proce[i][0] == proce[j][0])
{
if (intersection(selects[i], selects[j]))
{
cout << "此文法不是LL(1)文法, 原因如下:" << endl;
cout << "select ( " << proce[i][0] << "->" << proce[i].substr(1) << " ) = ";
cout << "{ ";
for (int k = 0; k < selects[i].size(); k++)
cout << gtchar[selects[i][k] - '0'] << " ";
cout << "}" << endl;
cout << "select ( " << proce[j][0] << "->" << proce[j].substr(1) << " ) = ";
cout << "{ ";
for (int k = 0; k < selects[j].size(); k++)
cout << gtchar[selects[j][k] - '0'] << " ";
cout << "}" << endl;
cout << "两个产生式的交集不为空集!" << endl;
return 0;
}
}
}
}
return 1;
}
6. 句子合法性分析
cpp复制代码bool analyze()
{
stack<char> sta;
sta.push('#');
sta.push(proce[0][0]);
int i = 0;
while (!sta.empty())
{
int cur = sta.top();
sta.pop();
if (cur == word[i])
{
i++;
}
else if (cur == '#')
{
return 1;
}
else if (table[gtnum[cur]][gtnum[word[i]]] != -1)
{
int k = table[gtnum[cur]][gtnum[word[i]]];
for (int j = proce[k].size() - 1; j > 0; j--)
{
if (proce[k][j] != '@')
sta.push(proce[k][j]);
}
}
else
{
return 0;
}
}
return 1;
}
源程序(逐行注释)
#include <bits/stdc++.h>
#define MaxSize 200
using namespace std;
/// 定义有关数据结构体
// const int MaxSize = 200; // 定义常量,表示数组最大长度
map<char, int> gtnum; // 获得对应编号
map<int, char> gtchar; // 获得对应字符
vector<string> proce; // 定义文法集合
int table[MaxSize][MaxSize]; // 预测分析表
int num = 0; // 字符计数器
int numvt = 0; // numvt是终结符的个数,
string word; // 存放输入的字符串
string first[MaxSize]; // 定义first集合
string follow[MaxSize]; // 定义follow集合
string selects[MaxSize]; // 定义select集合
/// 定义文法
string datas = R"(E->AXF|XF
F->AXF|@
X->YZ
Z->CYZ|@
Y->b|z|(E)
A->+|-
C->*|/
end)";
///
string endchar = R"(+ - * / ( ) b z
)";
string noendchar = R"(E F X Z Y A C
)";
/// 读入函数
void readin()
{
stringstream datascin(datas);
stringstream endcin(endchar);
stringstream noendcin(noendchar);
memset(table, -1, sizeof(table));
gtnum['#'] = 0;
gtchar[0] = '#';
// cout << "请输入该文法包含的所有终结符:" << endl;
char x;
do
{
endcin >> x;
gtnum[x] = ++num;
gtchar[num] = x;
} while (endcin.peek() != '\n');
numvt = ++num;
gtnum['@'] = numvt; // 空,用@表示
gtchar[num] = ('@');
// cout << "请输入该文法包含的所有非终结符:" << endl;
do
{
noendcin >> x;
gtnum[x] = ++num;
gtchar[num] = x;
} while (noendcin.peek() != '\n');
// cout << "输入要判断的文法(空字用'@'表示),以'end'结束:" << endl;
string pro;
while (datascin >> pro && pro != "end")
{
string ss;
ss += pro[0];
for (int i = 3; i < pro.size(); i++)
{
if (pro[i] == '|')
{
proce.push_back(ss);
ss.clear();
ss += pro[0];
}
else
{
ss += pro[i];
}
}
proce.push_back(ss);
}
}
/// 定义交集函数
void Union(string &a, string b) // a=a or b 取a,b交集赋值给a
{
set<char> se;
for (int i = 0; i < a.size(); i++)
se.insert(a[i]);
for (int i = 0; i < b.size(); i++)
se.insert(b[i]);
string ans;
set<char>::iterator it;
for (it = se.begin(); it != se.end(); it++)
ans += *it;
a = ans;
}
/// 利用dfs返回first(Vn)-@集合,并且判断vn能否推出空字
string get_first(int vn, int &has_0) // dfs:vn能推出的不含空字的vt集合,并且判断vn能否推出空字
{
if (vn == numvt)
has_0 = 1;
if (vn < numvt)
return first[vn];
string ans;
for (int i = 0; i < proce.size(); i++)
{
if (gtnum[proce[i][0]] == vn)
ans += get_first(gtnum[proce[i][1]], has_0);
}
return ans;
}
/// 获得产生式
string get_proce(int i) // 由对应下标获得对应产生式。
{
if (i < 0)
return " "; // 无该产生式
string ans;
ans += proce[i][0];
ans += "->";
for (int j = 1; j < proce[i].size(); j++)
ans += proce[i][j];
return ans;
}
/// 定义first函数
void getfirst()
{
for (int i = 1; i <= numvt; i++)
{ // 终结符,first集是其本身。
first[i] += ('0' + i);
}
for (int j = 0; j < proce.size(); j++)
{ // 扫描所有产生式
int k = 0;
int has_0 = 0; // k扫瞄该产生式
do
{
has_0 = 0;
k++;
if (k == proce[j].size())
{ // 推到最后一个了,则附加空字
first[gtnum[proce[j][0]]] += ('0' + numvt);
break;
} // 合并之
Union(first[gtnum[proce[j][0]]], get_first(gtnum[proce[j][k]], has_0));
} while (has_0); // 到无法推出空字为止
}
}
/// 定义follow函数
void getfollow()
{
Union(follow[gtnum[proce[0][0]]], "0"); // 先添加'#';
for (int j = 0; j < proce.size(); j++)
{ // 扫所有产生式
for (int jj = 1; jj < proce[j].size(); jj++)
{ // 每个非终结符的follow集
if (gtnum[proce[j][jj]] <= numvt)
continue; // vt无follow集
int k = jj;
int has_0;
do
{
has_0 = 0;
k++;
if (k == proce[j].size())
{ // 都能推出空字,follow集=产生式左边的vn,
Union(follow[gtnum[proce[j][jj]]], follow[gtnum[proce[j][0]]]);
break;
}
Union(follow[gtnum[proce[j][jj]]], get_first(gtnum[proce[j][k]], has_0));
} while (has_0);
}
}
}
/// 定义select函数
void getselect()
{
// 扫描所有的产生式
for (int i = 0; i < proce.size(); i++)
{
// 直接推导出空的产生式
if (proce[i][1] == '@')
{
selects[i] = follow[gtnum[proce[i][0]]];
continue;
}
if (gtnum[proce[i][1]] < numvt)
{
selects[i] = first[gtnum[proce[i][1]]];
continue;
}
int flag1 = 0;
for (int j = 1; j < proce[i].size(); j++)
{
string tepf = first[gtnum[proce[i][j]]];
int flag2 = 1;
for (int k = 0; k < tepf.size(); k++)
{
if (tepf[k] == ('0' + numvt))
{
flag2 = 0;
break;
}
}
if (flag2)
{
Union(selects[i], tepf);
flag1 = 0;
break;
}
int has_0 = 0;
Union(selects[i], get_first(gtnum[proce[i][j]], has_0));
flag1 = 1;
}
if (flag1)
{
Union(selects[i], follow[gtnum[proce[i][0]]]);
}
}
}
/// 打印first函数
void print_first()
{
cout << endl
<< "该文法的first集如下:" << endl;
for (int i = 1; i <= num; i++)
{
cout << "first (" << gtchar[i] << ") = ";
cout << "{ ";
for (int j = 0; j < first[i].size(); j++)
cout << gtchar[first[i][j] - '0'] << " ";
cout << "}" << endl;
}
cout << endl;
}
/// 打印follow集合
void print_follow()
{
cout << "该文法的follow集如下:" << endl;
for (int i = numvt + 1; i <= num; i++)
{
cout << "follow (" << gtchar[i] << ") = ";
cout << "{ ";
for (int j = 0; j < follow[i].size(); j++)
cout << gtchar[follow[i][j] - '0'] << " ";
cout << "}" << endl;
}
cout << endl;
}
/// 打印select集合
void printselect()
{
cout << "该文法的select集如下:" << endl;
for (int i = 0; i < proce.size(); i++)
{
cout << "select ( " << proce[i][0] << "->" << proce[i].substr(1) << " ) = ";
cout << "{ ";
for (int j = 0; j < selects[i].size(); j++)
cout << gtchar[selects[i][j] - '0'] << " ";
cout << "}" << endl;
}
cout << endl;
}
/// 定义预测分析表
void gettable() // 得预测分析表
{
for (int i = 0; i < proce.size(); i++)
{ // 扫所有产生式
if (proce[i][1] == '@')
{ // 直接推出空字的,特判下(follow集=产生式左边的vn中元素填)
string flw = follow[gtnum[proce[i][0]]];
for (int k = 0; k < flw.size(); k++)
{
table[gtnum[proce[i][0]]][flw[k] - '0'] = i;
}
}
string temps = first[gtnum[proce[i][1]]];
for (int j = 0; j < temps.size(); j++)
{ // 考察first集
if (temps[j] != ('0' + numvt))
{
table[gtnum[proce[i][0]]][temps[j] - '0'] = i;
}
else
{ // 有空字的,考察follw集
string flw = follow[gtnum[proce[i][1]]];
for (int k = 0; k < flw.size(); k++)
{
table[gtnum[proce[i][0]]][flw[k] - '0'] = i;
}
}
}
}
}
/// 打印预测分析表
void print_table()
{
cout << endl
<< "该文法的预测分析表如下:" << endl;
for (int i = 0; i < numvt; i++)
cout << '\t' << gtchar[i];
cout << endl;
for (int i = numvt + 1; i <= num; i++)
{
cout << gtchar[i];
for (int j = 0; j < numvt; j++)
{
cout << '\t' << get_proce(table[i][j]);
}
cout << endl;
}
cout << endl;
}
/// 判断是否有交集
bool intersection(string a, string b)
{
for (int i = 0; i < a.size(); i++)
{
for (int j = 0; j < b.size(); j++)
{
if (a[i] == b[j])
return 1;
}
}
return 0;
}
/// 判断是否为LL(1)文法
// First集中含有ε的非终结符的Follow集与其First集交集是否为空
bool check_LL1()
{
for (int i = 0; i < proce.size(); i++)
{
for (int j = i + 1; j < proce.size(); j++)
{
if (proce[i][0] == proce[j][0])
{
if (intersection(selects[i], selects[j]))
{
cout << "此文法不是LL(1)文法, 原因如下:" << endl;
cout << "select ( " << proce[i][0] << "->" << proce[i].substr(1) << " ) = ";
cout << "{ ";
for (int k = 0; k < selects[i].size(); k++)
cout << gtchar[selects[i][k] - '0'] << " ";
cout << "}" << endl;
cout << "select ( " << proce[j][0] << "->" << proce[j].substr(1) << " ) = ";
cout << "{ ";
for (int k = 0; k < selects[j].size(); k++)
cout << gtchar[selects[j][k] - '0'] << " ";
cout << "}" << endl;
cout << "两个产生式的交集不为空集!" << endl;
return 0;
}
}
}
}
// cout << "此文法是LL(1)文法" << endl;
return 1;
}
/// 定义判断句子合法性函数
bool analyze() // 总控,分析字word的合法性,若合法,输出所有产生式。
{
// cout << endl
// << "分析所得的产生式如下:" << endl;
stack<char> sta;
sta.push('#');
sta.push(proce[0][0]);
int i = 0;
while (!sta.empty())
{
int cur = sta.top();
sta.pop();
if (cur == word[i])
{ // 是终结符,推进
i++;
}
else if (cur == '#')
{ // 成功,结束
return 1;
}
else if (table[gtnum[cur]][gtnum[word[i]]] != -1)
{ // 查表
int k = table[gtnum[cur]][gtnum[word[i]]];
// cout << proce[k][0] << "->";
// for (int j = 1; j < proce[k].size(); j++)
// cout << proce[k][j];
// cout << endl;
for (int j = proce[k].size() - 1; j > 0; j--)
{ // 逆序入栈
if (proce[k][j] != '@')
sta.push(proce[k][j]);
}
}
else
{ // 失败!
return 0;
}
}
return 1;
}
string getInFomula()
{
string res;
string temp;
int n = 0;
while (cin >> temp)
{
if (temp[temp.size() - 2] >= '0' && temp[temp.size() - 2] <= '9')
{
res += 'z';
}
else if (temp[temp.size() - 2] >= 'a' && temp[temp.size() - 2] <= 'z')
{
res += 'b';
}
else
res += temp[temp.size() - 2];
n++;
}
return res;
}
int main()
{
readin(); // 读入文法
getfirst(); // 获取此文法的first集
getfollow(); // 获取此文法的follow集
getfollow();
getselect(); // 获取此文法的Select集
gettable(); // 获取预测分析表
// print_first(); // 打印first集
// print_follow(); // 打印follow集
// printselect(); // 打印select集
// 判断是否是LL(1)文法
if (!check_LL1())
{
return 0;
};
// print_table(); // 打印此文法的预测表
// cout << "请输入一个字符串:" << endl;
// cin >> word;
word = getInFomula(); // 输入要分析的字符串
if (analyze())
cout << "Yes,it is correct." << endl;
else
cout << "No,it is wrong." << endl;
return 0;
}
调试数据
样例输入
(a+15)*b样例输出
(lparen,() (ident,a) (plus,+) (number,15) (rparen,)) (times,*) (ident,b) Yes,it is correct.运行结果
实验调试情况及体会
通过这次实验,我成功实现了LL(1)分析法进行语法分析,深刻体会到了其利用预测分析表和栈来进行符号匹配和选择产生式,从而推导出输入串语法结构的奥妙。
首先,我清晰地认识到LL(1)分析法的核心在于构建预测分析表。预测分析表由非终结符和终结符构成,通过它,我们可以根据当前栈顶符号和输入串首符号,快速确定应选择的产生式,从而进行语法推导。在实验中,我通过定义非终结符和终结符的数组,以及对预测分析表的初始化,成功构建了一个完整的预测分析表。这一步骤让我感受到逻辑推理的魅力,每一个细节都在逻辑中紧密相连,犹如编织一张精密的网。
其次,我深刻意识到LL(1)分析法对文法的严格要求。文法必须满足LL(1)的条件,即每个非终结符的每个产生式的选择集与其他产生式的选择集不能有交集,以确保在分析过程中不会出现二义性和回溯。实验中,我针对给定的文法,仔细检查每个非终结符的产生式,并根据LL(1)文法的条件进行了调整和修改。这一过程不仅让我对文法结构有了更深刻的理解,更让我感受到精益求精的追求和不断完善的动力。
在编写代码的过程中,我深入理解了LL(1)分析法的工作原理。通过构建analyze()函数,我实现了循环的语法分析过程。每次循环中,根据栈顶字符和输入串首字符进行匹配,并根据预测分析表选择相应的产生式。通过不断地匹配和选择产生式,逐步推导出输入串的语法结构。每一次成功匹配和推导,都让我体验到如同解谜般的成就感。
这次实验不仅让我对LL(1)分析法的应用有了更深刻的理解,还让我意识到它在编译原理中的重要性。LL(1)分析法不仅是构建抽象语法树的基石,更是生成中间代码的重要工具。通过这次实践,我不仅掌握了理论知识,更培养了严谨的思维方式和解决问题的能力。
这次实验让我真切感受到编译原理的魅力,也更加坚定了我对计算机科学的热爱。每一个细节的推敲,每一个逻辑的验证,都让我沉浸其中,乐在其中。感谢这次实验,让我在知识的海洋中遨游,收获颇丰。