

《编译原理实验》
实验报告
| 题 目 | : | 第三次实验 算符优先分析 |
| 姓 名 | : | 高星杰 |
| 学 号 | : | 2021307220712 |
| 专 业 | : | 计算机科学与技术 |
| 上课时间 | : | 2024春 |
| 授课教师 | : | 刘善梅 |
2024 年 4月 25 日
[TOC]
编译原理 第三次实验 算符优先分析
实验目的
- 根据算符优先分析法,对表达式进行语法分析,使其能够判断一个表达式是否正确。
- 通过算符优先分析方法的实现,加深对自下而上语法分析方法的理解。
- 加深对语法分析器工作过程的理解;
- 加强对算符优先分析法实现语法分析程序的掌握;
- 能够采用一种编程语言实现简单的语法分析程序;
实验要求
- 根据简单表达式文法构造算符优先分析表
- 根据构造出来的算符优先分析表进行表达式的分析
- 能采用算符优先分析法对一个算术表达式(b+9)*a做自下而上的语法分析;
- 可自行设计一个算符优先文法,能识别含有句子(b+9)*a的语言;
- 也可基于PL/0语言的文法(完整文法参见本文档最后的附录)来做,若基于PL/0语言文法,需重点关注以下几条文法的EBNF,若不习惯看文法的巴科斯范式EBNF,可先将文法改写成常规的产生式形式P75。
分析对象〈算术表达式〉的BNF定义如下:
<表达式> ::= [+|-]<项>{<加法运算符> <项>} <项> ::= <因子>{<乘法运算符> <因子>} <因子> ::= <标识符>|<无符号整数>| ‘(’<表达式>‘)’ <加法运算符> ::= +|- <乘法运算符> ::= *|/ <关系运算符> ::= =|#|<|<=|>|>= <标识符> ::=<字母>{<字母>|<数字>} <无符号整数> ::= <数字>{<数字>} <字母> ::= a|b|…|X|Y|Z <数字> ::= 0|1|…|8|9
实验要求:
编程基础扎实的同学,建议用程序分别求解firstvt集和lastvt集,并用程序实现算符优先分析表;
编程基础非常非常薄弱的同学,可以人工求解firstvt集和lastvt集,人工设计好算符优先分析表,然后直接在程序中给出手工设计好的算符优先分析表。
编程基础尚可的同学,可根据自身情况编程firstvt集、lastvt集和算符优先分析表这三个部分的某些部分。(书上都有算法,建议同学们尽量用程序实现)
实验完成程度
本次实验我完成了一下功能:
| 实现的内容 | 实现的方式 |
|---|---|
| 求解firstvt集 | 程序实现 |
| 求解lastvt集 | 程序实现 |
| 求解算符优先分析表 | 程序实现 |
| 判断是否是简单优先文法 | 程序实现 |
| 使用算符优先分析过程 | 程序实现 |
| 是否仅支持PL/0文法 | 否、可以输出其他文法和句子进行判断 |
由于是先把算符优先分析实现了,先实现了一般形式的算符优先分析(可以自己输入产生式、和句子),所以在最后提交的时候,为了适应itc的输入输出格式,最后做出了一些输入输出格式的修改
设计思想
1 文法每个非终结符的 FIRSTVT 集和 LASTVT 集
FirstLast 类用于 FIRSTVT 集合和 LASTVT 集合构造。
主要数据:
- first:char[][] 用于存储非终结符的 FIRSTVT 集合
- last:char[][] 用于存储非终结符的 LASTVT 集合
对 FIRSTVT 集的构造我们可以给出一个算法,这个算法基于下面两条规则:
- 若有产生式 A→a…或 A→Ba…,则 a 属于 FIRSTVT(A),其中 A,B为非终结符,a 为终结符
- 若 a 属于 FIRSTVT(B)且有产生式 A→B…则有 a 属于 FIRSTVT(A)
为了计算方便,我们建立一个布尔数组 F[m,n](m 为非终结符个数,n 为终结符个数)和一个后进先出栈 STACK。我们将所有的非终结符排序,用的序号,再将所有的终结符排序,用 表示终结符 a 的序号。算法的目的是要合数组每一个元素最终取什满足:F[ , ]的值为真,当且仅当 a 属于 FIRSTVT(A)。至此,显然所有非终结符的 FIRSTVT 集己完全确定。
步骤如下:
- 首先按规则(1)对每个数组元素赋初值。观察这些初值,若 F [ Ai , aj ]的值为真,则将(A ,a)推入栈中,直至对所有数组元素的初值都按此处处理完
- 然后对栈做以下运算
- 将栈顶项弹出,设为(B,a),再用规则(2)检查所有产生式,若有形为 A→B…的产生式,而 F [ Ai , aj ]的值是假,则令其变为真,且将(A ,a)推进栈,如此重复直到栈弹空为止
具体的算法可用程序描述为:
PROCEDURE INSERT(A,a)
IF NOT F [ Ai , aj ] THEN
BEGIN
F[ Ai , aj ]:=TRUE
PUSH(A,a) ONTO STACK
END
此过程用于当 a 属于 FIRSTVT(A)时置 F[ Ai, aj ]为真,并将符号对(A, a)下推到栈中,其主程序为:
BEGIN (MAIN)
FOR I 从 1 到 m,j 从 1 到 n
DO F[ Ai , aj ] :=FALSE;
FOR 每个形如 A→a…或 A→Ba…的产生式
DO INSERT(A,a)
WHILE STACK 非空 DO
BEGIN
把 STACK 的顶项记为(B,a)弹出去
FOR 每个形如 A→B…的产生式
DO INSERT(A,a)
END
END (MAIN)
利用类似的方法可求得每个非终结符的 LASTVT(A)。
2 由 LASTVT 和 FIRSTVT 集建立优先矩阵
Table 类利用之前构造的 LASTVT 和 FIRSTVT 生成。
主要数据:
- table: int[][] 用于存储算符优先关系矩阵
有了文法中的每个非终结符的 FIRSTVT 集和 LASTVT 集,我们就可以用如下算法最后构造文法的优先关系表:
FOR 每个产生式 A→ X1 X2… Xn DO
FOR i:=1 TO n-1 DO
BEGIN
IF Xi 和 Xi+1均为终结符
THEN 置 Xi = Xi+1
IF Xi 和 Xi+2都为终结符,但 Xi+1为非终结符
THEN 置 Xi = Xi+2;
IF Xi 为终结符而 Xi+1为非中介符
THEN FOR FIRSTFVT( Xi+1 )中的每个 b DO 置 Xi <b;
IF Xi 为非终结符而 Xi+1为终结符
THEN FOR LASTVT( Xi )中的每个 a DO 置 a> Xi+1
END
以上算法对任何算符文法 G 可自动构造其算符优先关系表,并可判断 G 是否为算符优先关系。
3 算符文法的分析归约过程算法
自底向上的算符优先分析法,也为自左右向右归约,我们已经知道它不是规范归约。规范归约的关键问题是如何寻找当前句型的句柄,句柄为某一产生式的右面部,归约结果为用与句柄相同的产生式右面部之左部非终结符代替句柄,而算符优先分析归约的关键,是如何找最左素短语,而最左右素短语 Ni ai Ni+1。
ai+1…… aj Nj+1应满足:
- ai-1 <· ai
- ai = ai+1 =…… aj
- aj ·> aj+1
在文法的产生式中存在右面部符号串的符号个数与该素短语的符号个数相等,非终结符号对应 Nk ,(k=i,…,j+1)不管其符号名是什么。终结符对应 i a ,…, j a ,其符号表示要与实际的终结符相一致才有可能形成素短语。由此,我们在分析过程中可以设置一个符号栈 S,用以寄存归约或待形成最左素短语的符号串,用一个工作单元 a 存放当前读入的终结符号,归约成功的标志是当读到句子结束符#时,S 本中只剩#N,即只剩句子最左括号“#”和一非终结符 N。下面给出分析过程的示意图 在归约时要检查是否有对应产生式的右部与 S[j+1]…S[k]形式相符,(忽略非终结符名的不同)若有才可归约,否则出错。在这个分析过程中把“#”也放在终结符串中。
算符优先分析的移进规约流程图:
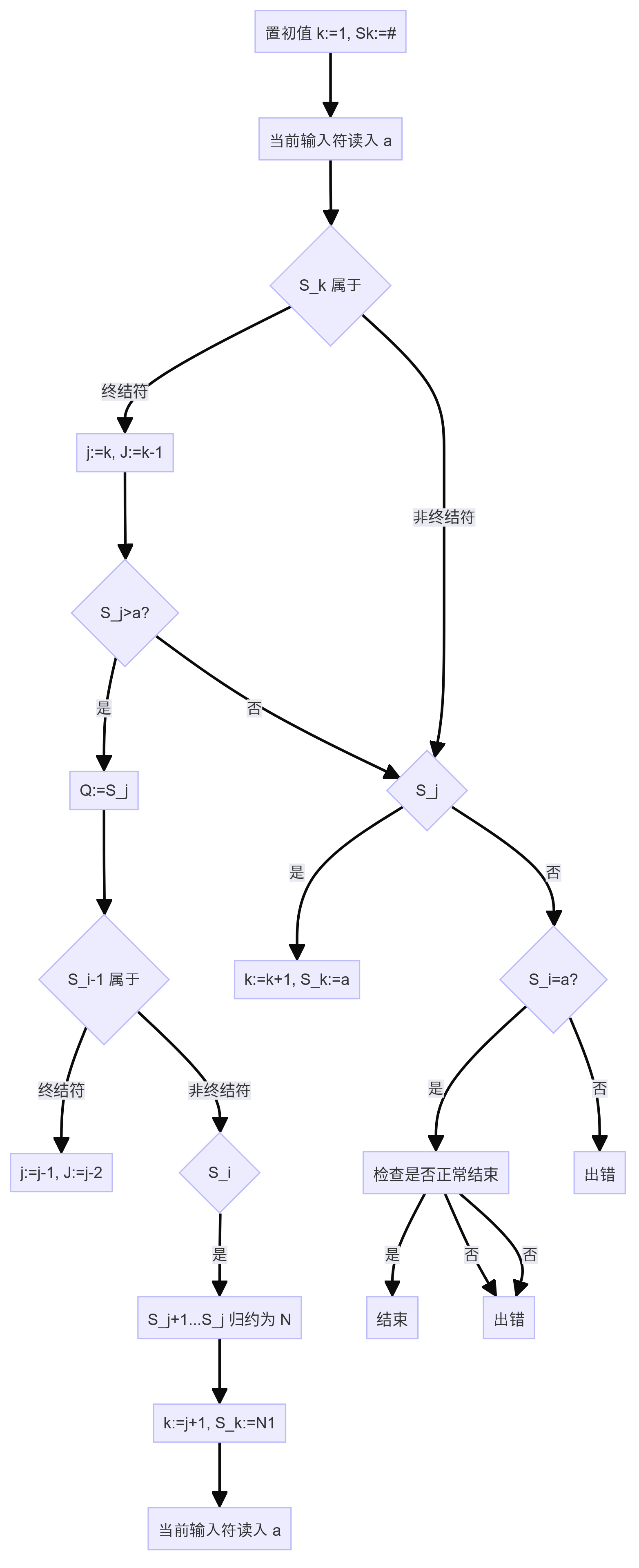
4 语法分析树
语法树是在对字串进行算符优先分析时同步生成的,一个子树对应一个最左速短语。语法树的每一次构建操作对应算符优先分析时的一个规约操作。
语法树根据算符优先规约的规则和逻辑,以自下而上的顺序生成每次算符优先分析时要对 S[j+1]…S[k]规约为某个 N 时,记录下要规约的 S[j+1]…S[k]字符作为当前一个子树的叶子节点,N 作为当前子树的根节点建立父子关系。
将 S[j+1]…S[k]规约成的 N,存入一个栈中(代码中使用一个指针数组实现),保存下来,作为之后规约操作时一个子树的叶节点。
循环执行后,在最后一步规约时,将 S[j+1]…S[k]规约成的 N 作为语法树的根节点 root。
将建立好的语法树逻辑结构,带入多叉树建立算法中,生成语法树,并打印出来。
算法流程
算符优先文法的执行过程为:输入已知文法,分析其正确性,提取非终结符和终结符,构造非终结符的 FIRSTVT 集和 LASTVT 集,再次基础上构造算符优先关系矩阵,并用来判断表达式是否符合该文法。
算符优先文法程序总的流程图为:

这个算符优先分析程序的算法流程如下:
1. 数据结构初始化
- 定义变量和数据结构:
table[20][20]:存储算符优先关系表。grammar[10][30]:存储文法产生式。FIRSTVT[10][10]和LASTVT[10][10]:存储每个非终结符的FirstVT和LastVT集合。T_label[20]:存储所有的终结符。input_s[100]:存储待分析的输入串。s[100]:用于语法分析的栈。
2. 读取文法规则
- 从输入中读取文法产生式,直到遇到结束符号
#。在读取过程中,初始化FIRSTVT和LASTVT。
printf("输入产生式,以#结束");
for (i = 0;; i++) {
scanf("%s", grammar[i]);
FIRSTVT[i][0] = 0;
LASTVT[i][0] = 0;
for (j = 0; grammar[i][j]; j++) {
if (grammar[i][j] == '#') {
if (j) r = i + 1;
else r = i;
grammar[i][j] = '\0';
break;
}
}
if (grammar[i][j] == '#') break;
}
3. 判断是否为算符文法
- 检查每个产生式,确保符合算符文法的定义:
- 每个产生式的左部必须是一个单一的非终结符。
- 每个产生式的右部不能有连续的非终结符。
for (i = 0; i < r; i++) {
for (j = 0; grammar[i][j] != '\0'; j++) {
if (grammar[i][0] < 'A' || grammar[i][0] > 'Z') {
printf("该文法不是算符文法\n!");
exit(-1);
}
if (grammar[i][j] >= 'A' && grammar[i][j + 1] >= 'A' && grammar[i][j + 1] <= 'Z') {
printf("该文法不是算符文法\n!");
exit(-1);
}
}
}
4. 收集终结符
- 在读取文法规则的过程中,收集所有的终结符并存储在
T_label数组中。
for (i = 0; i < r; i++) {
for (j = 0; grammar[i][j] != '\0'; j++) {
if ((grammar[i][j] < 'A' || grammar[i][j] > 'Z') && grammar[i][j] != '-' && grammar[i][j] != '>' && grammar[i][j] != '|') {
T_label[k++] = grammar[i][j];
}
}
}
T_label[k] = '#';
T_label[k + 1] = '\0';
5. 生成FIRSTVT和LASTVT集合
- 对于每个非终结符,递归计算其FIRSTVT和LASTVT集合。通过遍历文法产生式,判断并合并相应的终结符。
for (i = 0; i < r; i++) {
firstvt(grammar[i][0]);
lastvt(grammar[i][0]);
}
6. 生成算符优先关系表
- 根据文法规则,推导出终结符之间的优先关系,并填入
table中。- 若
a和b均为终结符且相邻,则a = b。 - 若
a为终结符,B为非终结符且B的FIRSTVT集中包含终结符b,则a < b。 - 若
A为非终结符,b为终结符且A的LASTVT集中包含终结符a,则a > b。 - 特殊处理
#与其他符号的关系。
- 若
void P_table() {
// 生成FIRSTVT和LASTVT
for (i = 0; i < r; i++) {
firstvt(grammar[i][0]);
lastvt(grammar[i][0]);
}
// 生成优先关系表
for (i = 0; i < r; i++) {
// 遍历文法规则,填表
}
// 处理#与其他符号的关系
m = index('#');
for (t = 0; t < FIRSTVT[0][0]; t++) {
n = index(FIRSTVT[0][t + 1]);
table[m][n] = '<';
}
n = index('#');
for (t = 0; t < LASTVT[0][0]; t++) {
m = index(LASTVT[0][t + 1]);
table[m][n] = '>';
}
table[n][n] = '=';
}
7. 输出FIRSTVT和LASTVT集合
- 输出每个非终结符的FIRSTVT和LASTVT集合。
printf("\nFIRSTVT集\n");
for (i = 0; i < r; i++) {
printf("%c: ", grammar[i][0]);
for (j = 0; j < FIRSTVT[i][0]; j++) {
printf("%c ", FIRSTVT[i][j + 1]);
}
printf("\n");
}
printf("\nLASTVT集\n");
for (i = 0; i < r; i++) {
printf("%c: ", grammar[i][0]);
for (j = 0; j < LASTVT[i][0]; j++) {
printf("%c ", LASTVT[i][j + 1]);
}
printf("\n");
}
8. 输出算符优先关系表
- 输出算符优先分析表,显示各终结符之间的优先关系。
printf("\n算符优先分析表:\n");
for (i = 0; T_label[i] != '\0'; i++) printf("\t%c", T_label[i]);
printf("\n");
for (i = 0; i < k + 1; i++) {
printf("%c\t", T_label[i]);
for (j = 0; j < k + 1; j++) {
printf("%c\t", table[i][j]);
}
printf("\n");
}
9. 输入待分析字符串
- 读取待分析的输入串。
printf("\n输入单词串\n");
scanf("%s", input_s);
10. 语法分析过程
- 初始化分析栈,将
#压入栈底,开始逐步分析输入串。 - 根据栈顶符号和当前输入符号的优先关系,选择进行移进或规约操作。
- 移进:将当前输入符号移入栈,并继续读取下一个输入符号。
- 规约:根据文法规则进行规约操作,将栈顶符号规约为对应的非终结符。
- 在规约过程中,同时构建语法树,记录规约过程的节点关系。
int test_s() {
k = 1;
s[k] = '#';
printf("栈 输入串 动作\n");
while ((a = input_s[i]) != '\0') {
if (is_T(s[k])) j = k;
else j = k - 1;
x = index(s[j]);
y = index(a);
if (table[x][y] == '>') {
stack_p(1, k, s);
printf("%c", a);
stack_p(i + 1, z, input_s);
printf("规约\n");
// 进行规约操作并更新栈
}
else if (table[x][y] == '<' || table[x][y] == '=') {
stack_p(1, k, s);
printf("%c", a);
stack_p(i + 1, z, input_s);
printf("移进\n");
k++;
s[k] = a;
i++;
}
else {
printf("\n该单词串不是该文法的句子\n");
return 0;
}
}
printf("\n该单词串不是该文法的句子\n");
return 0;
}
11. 生成并打印语法树
- 如果规约成功,生成语法树并打印。
if (k == 2 && a == '#') {
stack_p(1, k, s);
printf("%c", a);
stack_p(i + 1, z, input_s);
printf("接受\n");
printf("accept\n");
printf("\n生成的语法树: \n");
printTree(sn[sn_c],
0, 0);
deleteTree(sn[sn_c]);
return 1; // 规约成功
}
源程序
#include <bits/stdc++.h>
using namespace std;
int state[100];
int sn_c = 0;
/*
E->E+T|T
T->T*F|F
F->(E)|i
#
(b+9)*a
(b+8)+*a#
*/
/*
E->E+T|T
T->T*F|F
F->P^F|P
P->(E)|i
S->a|^|(T)
T->T,S|S
*/
//.............................
char table[20][20]; // 算符优先关系表
char s[100];
char str_in[20][10];
char T_label[20];
char input_s[100];
int FVT[10] = {0};
int LVT[10] = {0};
int k, j;
char a, q;
int r; // 文法规则个数
int r1;
int m, n, N;
char grammar[10][30]; // 用来存储文法产生式
char FIRSTVT[10][10]; // FIRSTVT集
char LASTVT[10][10]; // LASTVT集
int test_s(); // 字串分析
int is_T(char c);
int index(char c);
void stack_p(int j, int k, char *s); // 打印
void firstvt(char c); // 求FIRSTVT集
void lastvt(char c); // 求LASTVT集
void P_table(); // 生成算符文法优先关系表
typedef struct TNode
{
char *table;
int n;
struct TNode *child[10];
} TreeNode;
void printTree(TreeNode *root, int depth, unsigned char flag)
{
int i, tmp;
unsigned char newflag;
for (i = 0; i < depth; ++i)
{
switch (state[i])
{
case 0:
printf(" ");
break;
case 1:
printf("│");
break;
case 3:
printf("├");
break;
case 4:
printf("└");
break;
case 2:
printf("─");
break;
default:;
}
if (i < depth - 1)
printf(" ");
else
printf("─");
}
printf("%s\n", root->table);
if (depth > 0)
{
if (flag & 1)
state[depth - 1] = 0;
else if (flag & 2)
state[depth - 1] = 1;
}
if (root->n == 0)
return;
for (i = 0; i < root->n; ++i)
{
newflag = 0;
if (i == 0)
newflag |= 2;
if (i == root->n - 1)
{
newflag |= 1;
state[depth] = 4;
}
else
state[depth] = 3;
tmp = state[depth - 1];
if (state[depth - 1] != 0 && state[depth - 1] != 1)
state[depth - 1] = 1;
// printTree(root->child[i], depth + 1, newflag);
state[depth - 1] = tmp;
}
}
void add_node(TreeNode *node, TreeNode *sub)
{
node->child[node->n++] = sub;
}
void deleteTree(TreeNode *root)
{
int i;
if (!root)
return;
for (i = 0; i < root->n; ++i)
deleteTree(root->child[i]);
free(root);
}
TreeNode *new_node(char *table)
{
TreeNode *node = (TreeNode *)malloc(sizeof(TreeNode));
node->table = table;
node->n = 0;
return node;
}
TreeNode *sn[20];
void P_table()
{
char text[20][10];
int i, j, k, t, l, x = 0, y = 0;
int m, n;
x = 0;
for (i = 0; i < r; i++)
{
firstvt(grammar[i][0]);
lastvt(grammar[i][0]);
}
for (i = 0; i < r; i++)
{
text[x][y] = grammar[i][0];
y++;
for (j = 1; grammar[i][j] != '\0'; j++)
{
if (grammar[i][j] == '|')
{
text[x][y] = '\0';
x++;
y = 0;
text[x][y] = grammar[i][0];
y++;
text[x][y++] = '-';
text[x][y++] = '>';
}
else
{
text[x][y] = grammar[i][j];
y++;
}
}
text[x][y] = '\0';
x++;
y = 0;
}
r1 = x;
// printf("产生式展开\n");
// for (i = 0; i < x; i++)
// {
// printf("%s\n", text[i]);
// }
for (i = 0; i < x; i++)
{
str_in[i][0] = text[i][0];
for (j = 3, l = 1; text[i][j] != '\0'; j++, l++)
str_in[i][l] = text[i][j];
str_in[i][l] = '\0';
}
for (i = 0; i < x; i++)
{
for (j = 1; text[i][j + 1] != '\0'; j++)
{
if (is_T(text[i][j]) && is_T(text[i][j + 1]))
{
m = index(text[i][j]);
n = index(text[i][j + 1]);
if (table[m][n] == '=' | table[m][n] == '<' | table[m][n] == '>')
{
printf("该文法不是算符优先文法\n");
exit(-1);
}
table[m][n] = '=';
}
if (text[i][j + 2] != '\0' && is_T(text[i][j]) && is_T(text[i][j + 2]) && !is_T(text[i][j + 1]))
{
m = index(text[i][j]);
n = index(text[i][j + 2]);
if (table[m][n] == '=' | table[m][n] == '<' | table[m][n] == '>')
{
printf("该文法不是算符优先文法\n");
exit(-1);
}
table[m][n] = '=';
}
if (is_T(text[i][j]) && !is_T(text[i][j + 1]))
{
for (k = 0; k < r; k++)
{
if (grammar[k][0] == text[i][j + 1])
break;
}
m = index(text[i][j]);
for (t = 0; t < FIRSTVT[k][0]; t++)
{
n = index(FIRSTVT[k][t + 1]);
if (table[m][n] == '=' | table[m][n] == '<' | table[m][n] == '>')
{
printf("该文法不是算符优先文法\n");
exit(-1);
}
table[m][n] = '<';
}
}
if (!is_T(text[i][j]) && is_T(text[i][j + 1]))
{
for (k = 0; k < r; k++)
{
if (grammar[k][0] == text[i][j])
break;
}
n = index(text[i][j + 1]);
for (t = 0; t < LASTVT[k][0]; t++)
{
m = index(LASTVT[k][t + 1]);
if (table[m][n] == '=' | table[m][n] == '<' | table[m][n] == '>')
{
printf("该文法不是算符优先文法\n");
exit(-1);
}
table[m][n] = '>';
}
}
}
}
m = index('#');
for (t = 0; t < FIRSTVT[0][0]; t++)
{
n = index(FIRSTVT[0][t + 1]);
table[m][n] = '<';
}
n = index('#');
for (t = 0; t < LASTVT[0][0]; t++)
{
m = index(LASTVT[0][t + 1]);
table[m][n] = '>';
}
table[n][n] = '=';
}
void firstvt(char c)
{
int i, j, k, m, n;
for (i = 0; i < r; i++)
{
if (grammar[i][0] == c)
break;
}
if (FVT[i] == 0)
{
n = FIRSTVT[i][0] + 1;
m = 0;
do
{
if (m == 2 || grammar[i][m] == '|')
{
if (is_T(grammar[i][m + 1]))
{
FIRSTVT[i][n] = grammar[i][m + 1];
n++;
}
else
{
if (is_T(grammar[i][m + 2]))
{
FIRSTVT[i][n] = grammar[i][m + 2];
n++;
}
if (grammar[i][m + 1] != c)
{
firstvt(grammar[i][m + 1]);
for (j = 0; j < r; j++)
{
if (grammar[j][0] == grammar[i][m + 1])
break;
}
for (k = 0; k < FIRSTVT[j][0]; k++)
{
int t;
for (t = 0; t < n; t++)
{
if (FIRSTVT[i][t] == FIRSTVT[j][k + 1])
break;
}
if (t == n)
{
FIRSTVT[i][n] = FIRSTVT[j][k + 1];
n++;
}
}
}
}
}
m++;
} while (grammar[i][m] != '\0');
FIRSTVT[i][n] = '\0';
FIRSTVT[i][0] = --n;
FVT[i] = 1;
}
}
void lastvt(char c)
{
int i, j, k, m, n;
for (i = 0; i < r; i++)
{
if (grammar[i][0] == c)
break;
}
if (LVT[i] == 0)
{
n = LASTVT[i][0] + 1;
m = 0;
do
{
if (grammar[i][m + 1] == '\0' || grammar[i][m + 1] == '|')
{
if (is_T(grammar[i][m]))
{
LASTVT[i][n] = grammar[i][m];
n++;
}
else
{
if (is_T(grammar[i][m - 1]))
{
LASTVT[i][n] = grammar[i][m - 1];
n++;
}
if (grammar[i][m] != c)
{
lastvt(grammar[i][m]);
for (j = 0; j < r; j++)
if (grammar[j][0] == grammar[i][m])
break;
for (k = 0; k < LASTVT[j][0]; k++)
{
int t;
for (t = 0; t < n; t++)
if (LASTVT[i][t] == LASTVT[j][k + 1])
break;
if (t == n)
{
LASTVT[i][n] = LASTVT[j][k + 1];
n++;
}
}
}
}
}
m++;
} while (grammar[i][m] != '\0');
LASTVT[i][n] = '\0';
LASTVT[i][0] = --n;
LVT[i] = 1;
}
}
int test_s()
{
int i, j, x, y, z;
k = 1;
s[k] = '#';
// printf("栈 输入串 动作\n");
for (i = 0; input_s[i] != '\0'; i++)
;
z = i--;
i = 0;
while ((a = input_s[i]) != '\0')
{
if (is_T(s[k]))
j = k;
else
j = k - 1;
x = index(s[j]);
y = index(a);
if (table[x][y] == '>')
{
stack_p(1, k, s);
// printf("%c", a);
stack_p(i + 1, z, input_s);
// printf("规约\n");
do
{
q = s[j];
if (is_T(s[j - 1]))
{
j = j - 1;
if (j <= 0)
{
// printf("输入串错误\n");
exit(-1);
}
}
else
{
j = j - 2;
if (j <= 0)
{
// printf("输入串错误\n");
exit(-1);
}
}
x = index(s[j]);
y = index(q);
} while (table[x][y] != '<');
int m, n, N;
int N1; // 存放规约符号标号
char tep[100]; // 存放最左素短语
for (int x = j + 1; x <= k; x++)
{
tep[x] = s[x];
}
for (m = j + 1; m <= k; m++)
{
for (N = 0; N < r1; N++)
for (n = 1; str_in[N][n] != '\0'; n++)
{
if (!is_T(s[m]) && !is_T(str_in[N][n]))
{
if (is_T(s[m + 1]) && is_T(str_in[N][n + 1]) && s[m + 1] == str_in[N][n + 1])
{
s[j + 1] = str_in[N][0];
N1 = N;
break;
}
}
else if (is_T(s[m]))
if (s[m] == str_in[N][n])
{
if (s[m] == '*' && m - 1 <= j)
{
// printf("\n该单词串不是该文法的句子\n");
return 0;
}
s[j + 1] = str_in[N][0];
N1 = N;
break;
}
}
}
//.................
// N为根节点,s[j+1--k]为子节点
char *c_n = new char[2];
c_n[0] = str_in[N1][0];
c_n[1] = '\0';
TreeNode *s2 = new_node(c_n);
for (int x = k; x >= j + 1; x--)
{
char *c_t = new char[2];
c_t[0] = tep[x];
c_t[1] = '\0';
TreeNode *s1 = new_node(c_t);
if (tep[x] >= 'A' && tep[x] <= 'Z')
{
add_node(s2, sn[sn_c]);
sn_c--;
}
else
{
add_node(s2, s1);
}
}
sn_c++;
sn[sn_c] = s2;
//......................
k = j + 1;
if (k == 2 && a == '#')
{
stack_p(1, k, s);
// printf("%c", a);
stack_p(i + 1, z, input_s);
// printf("接受\n");
// printf("accept\n");
// printf("\n生成的语法树: \n");
// printTree(sn[sn_c], 0, 0);
deleteTree(sn[sn_c]);
return 1; // 规约成功
}
}
else if (table[x][y] == '<' || table[x][y] == '=')
{ // 移进操作
stack_p(1, k, s);
// printf("%c", a);
stack_p(i + 1, z, input_s);
// printf("移进\n");
k++;
s[k] = a;
i++;
}
else
{
// printf("\n该单词串不是该文法的句子\n");
return 0;
}
}
// printf("\n该单词串不是该文法的句子\n");
return 0;
}
void stack_p(int j, int k, char *s)
{
int n = 0;
int i;
for (i = j; i <= k; i++)
{
// printf("%c", s[i]);
n++;
}
for (; n < 15; n++)
{
// printf(" ");
}
}
int index(char c) // 计算下标
{
int i;
for (i = 0; T_label[i] != '\0'; i++)
{
if (c == T_label[i])
return i;
}
return -1;
}
int is_T(char c) // 判断非终结符
{
int i;
for (i = 0; T_label[i] != '\0'; i++)
{
if (c == T_label[i])
return 1;
}
return 0;
}
void initial()
{
string temps[4] = {"E->E+T|T", "T->T*F|F", "F->(E)|i", "#"};
for (int i = 0; i < 4; i++)
{
int j;
for (j = 0; j < temps[i].size(); j++)
{
grammar[i][j] = temps[i][j];
}
grammar[i][j] = '\0';
}
string temp;
string res;
int pos = 0;
while (cin >> temp && pos < 7)
{
if (temp[temp.size() - 2] >= '0' && temp[temp.size() - 2] <= '9' || (temp[temp.size() - 2] >= 'a' && temp[temp.size() - 2] <= 'z'))
{
res += 'i';
}
else
res += temp[temp.size() - 2];
n++;
pos++;
}
res += '#';
for (int i = 0; i < res.size(); i++)
{
input_s[i] = res[i];
}
}
int main()
{
int i, j, k = 0;
r = 0;
bool flag = 0;
// printf("输入产生式,以#结束");
// S->a|^|(T)
// T->T,S|S
initial();
for (i = 0;; i++)
{
// scanf("%s", grammar[i]);
FIRSTVT[i][0] = 0;
LASTVT[i][0] = 0;
for (j = 0; grammar[i][j]; j++)
if (grammar[i][j] == '#')
{
if (j)
r = i + 1;
else
r = i;
flag = 1;
grammar[i][j] = '\0';
break;
}
if (flag)
break;
}
for (i = 0; i < r; i++) // 判断是否为算符文法
{
for (j = 0; grammar[i][j] != '\0'; j++)
{
if (grammar[i][0] < 'A' || grammar[i][0] > 'Z')
{
// printf("该文法不是算符文法\n!");
exit(-1);
}
if (grammar[i][j] >= 'A' && grammar[i][j] <= 'Z')
{
if (grammar[i][j + 1] >= 'A' && grammar[i][j + 1] <= 'Z')
{
// printf("该文法不是算符文法\n!");
exit(-1);
}
}
}
}
for (i = 0; i < r; i++)
{
for (j = 0; grammar[i][j] != '\0'; j++)
{
if ((grammar[i][j] < 'A' || grammar[i][j] > 'Z') && grammar[i][j] != '-' && grammar[i][j] != '>' && grammar[i][j] != '|')
T_label[k++] = grammar[i][j];
}
}
T_label[k] = '#';
T_label[k + 1] = '\0';
P_table();
// printf("\nFIRSTVT集\n");
// for (i = 0; i < r; i++)
// {
// printf("%c: ", grammar[i][0]);
// for (j = 0; j < FIRSTVT[i][0]; j++)
// {
// printf("%c ", FIRSTVT[i][j + 1]);
// }
// printf("\n");
// }
// printf("\nLASTVT集\n");
// for (i = 0; i < r; i++)
// {
// printf("%c: ", grammar[i][0]);
// for (j = 0; j < LASTVT[i][0]; j++)
// {
// printf("%c ", LASTVT[i][j + 1]);
// }
// printf("\n");
// }
// printf("\n算符优先分析表:\n");
// for (i = 0; T_label[i] != '\0'; i++)
// printf("\t%c", T_label[i]);
// printf("\n");
// for (i = 0; i < k + 1; i++)
// {
// printf("%c\t", T_label[i]);
// for (j = 0; j < k + 1; j++)
// {
// printf("%c\t", table[i][j]);
// }
// printf("\n");
// }
// printf("\n输入单词串\n");
// scanf("%s", input_s);
// for (int i = 0; i < 100; i++)
// {
// if ((input_s[i] >= 'a' && input_s[i] <= 'z') || (input_s[i] >= '0' && input_s[i] <= '9'))
// {
// input_s[i] = 'i';
// }
// }
if (test_s())
{
cout << "Yes,it is correct." << endl;
}
else
{
cout << "No,it is wrong." << endl;
}
return 0;
}
调试数据
样例输入
(lparen,()
(ident,b)
(plus,+)
(number,9)
(rparen,))
(times,\*)
(ident,a)
样例输出
Yes,it is correct.
运行结果
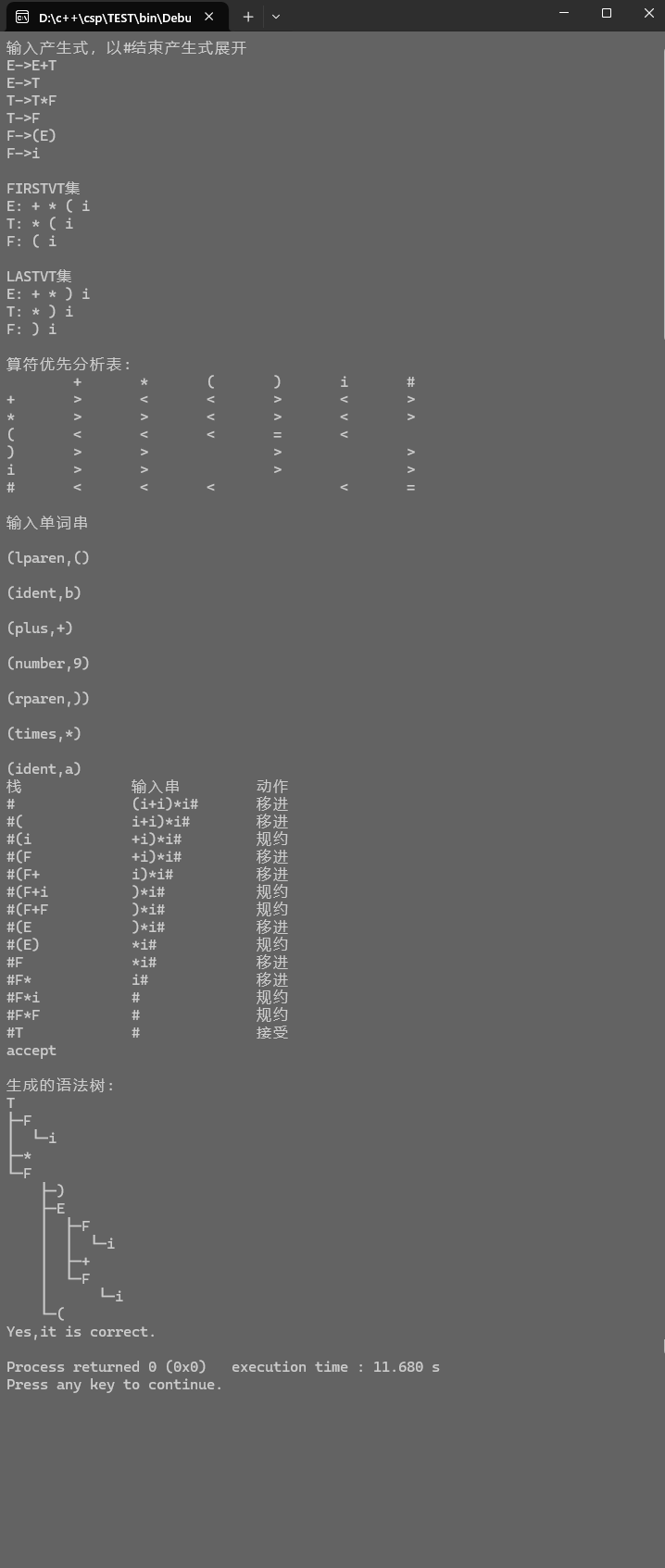
实验调试情况及体会
在这个算符优先文法的实验过程中,我深刻体会到了程序设计的复杂性。尤其是在数据结构的设计阶段,耗费了大量的时间和精力。选择合适的数据结构来满足程序需求,这一步远比我想象中要困难得多。
回想起最初的几天,我一直在不同的数据结构之间反复权衡和尝试。每一种选择都需要考虑它的优缺点,如何才能最好地支持接下来的程序编写。这个过程充满了反复和不确定性,但也正是这个过程,让我对数据结构有了更深入的理解。
一旦数据结构确定下来,程序编写的过程就显得相对顺利了许多。看到程序能够对正确的输入做出正确的处理,内心有一种难以言表的成就感。然而,事情并没有那么简单。程序还缺乏查错纠错的能力,这使得它在面对错误输入时显得无力。这也是我在这次实验中最大的挑战之一。
为了增加查错纠错功能,我花费了大量的时间和精力。每次遇到问题,我都不得不重新思考程序的逻辑,调整代码,进行无数次的调试。这段时间的工作虽然艰难,但也让我学会了如何更好地处理错误,如何使程序更加健壮和可靠。
在整个编程过程中,我逐渐意识到,编写代码不仅仅是技术上的挑战,更是一种艺术。需要在理性与感性之间找到平衡,既要严谨细致,又要灵活变通。调试的过程虽然痛苦,但每次成功解决一个问题,都让我感到无比的喜悦。
这次实验不仅让我在技术上有所提升,更让我在心态上得到了磨炼。我学会了如何面对复杂的问题,如何在困境中找到解决的办法。这段经历让我对编程有了新的认识和更深的热爱。尽管过程艰难,但我为自己最终完成任务感到自豪。
感谢这次实验,让我在编程的道路上迈出了重要的一步。未来,我将继续努力,不断提升自己的技能,迎接更多的挑战。