

《编译原理实验》
实验报告
| 题 目 | : | 第四次实验 LR分析法 |
| 姓 名 | : | 高星杰 |
| 学 号 | : | 2021307220712 |
| 专 业 | : | 计算机科学与技术 |
| 上课时间 | : | 2024春 |
| 授课教师 | : | 刘善梅 |
2024 年 6月 13 日
[TOC]
编译原理 第四次实验 自下而上语法分析2(LR分析法)
实验目的
- 能采用LR分析法对一个算术表达式(b+9)*a做自下而上的语法分析;
- 可自行设计一个LR文法,能识别含有句子(b+9)*a的语言;
- 也可基于PL/0语言的文法(完整文法参见本文档最后的附录)来做,若基于PL/0语言文法,需重点关注以下几条文法的EBNF,若不习惯看文法的巴科斯范式EBNF,可先将文法改写成常规的产生式形式P75。
分析对象〈算术表达式〉的EBNF定义如下:
<表达式> ::= [+|-]<项>{<加法运算符> <项>} <项> ::= <因子>{<乘法运算符> <因子>} <因子> ::= <标识符>|<无符号整数>| ‘(’<表达式>‘)’ <加法运算符> ::= +|- <乘法运算符> ::= *|/ <关系运算符> ::= =|#|<|<=|>|>= <标识符> ::=<字母>{<字母>|<数字>} <无符号整数> ::= <数字>{<数字>} <字母> ::= a|b|…|X|Y|Z <数字> ::= 0|1|…|8|9
实验要求
- 编程基础较扎实的同学,建议用程序构造文法的LR(0)项目集规范族(构造算法见教材P107);判断文法是LR(0)、SLR和LR(1)中的哪一种,然后用程序构造LR分析表(LR(0)分析表构造算法P109;SLR分析表构造算法P112;LR(1)构造算法P115);
- 编程基础非常非常薄弱的同学,可以人工求解LR(0)项目集规范族,判断文法是LR(0)、SLR和LR(1)中的哪一种,构造LR分析表,然后直接在程序中给出手工设计好的LR分析表。
- 编程基础尚可的同学,可根据自身情况编程构造文法的LR(0)项目集规范族、构造LR分析表(书上都有算法,建议同学们尽量用程序实现)
实验完成程度
由于本次实验给出的样例文法直接使用LR(0)分析会产生冲突不能正确判断句子,所以在LR(0)的基础上实现了SLR(1)分析,最终成功解决了LR(0)的分析。
| 实现的内容 | 实现的方式 |
|---|---|
| 实现文法SLR(1) | 程序实现 |
| 求解闭包 | 程序实现 |
| 求解转移goto | 程序实现 |
| 构建项目集规范族 | 程序实现 |
| 求解FIRST和FOLLOW集合 | 程序实现 |
| 构建分析表 | 程序实现 |
| 语法分析过程 | 程序实现 |
| 是否仅支持PL/0文法 | 否、可以输出其他文法和句子进行判断 |
设计思想
1. 文法扩展与预处理
1.1 文法表示
文法由以下部分组成:
q0:起始符号。vn:非终结符集合。vt:终结符集合。prods:产生式集合,每个产生式表示为(head, body)的形式。
1.2 增广文法
为简化分析过程,我们引入一个新的开始符号 FAKE_S,并添加相应的产生式。同时,增加终结符 EOF 作为输入结束符号。
1.3 生成初始项目
初始项目集从新引入的开始符号的产生式开始,表示项目 (0, 0),其中 0 表示产生式索引,0 表示项目点位置。
2. 闭包与转移函数
2.1 闭包函数 (closure)
对一个项目集进行扩展,包含所有可能的后续项目。
- 从当前项目集中的每个项目出发,找到点后面的符号。
- 对于每个非终结符,将其所有产生式作为新项目加入集合,直到不再有新的项目加入。
2.2 转移函数 (goto)
计算从一个项目集经过某个符号转移后到达的下一个项目集。
- 从当前项目集中选取点后符号为给定符号的项目,将点后移一位。
- 对这些新项目集合应用闭包操作,得到下一个项目集。
3. 构建项目集规范族
3.1 项目集规范族
通过不断应用转移函数,从初始项目集出发,构建整个项目集规范族。
- 使用集合保存所有已处理和未处理的项目集。
- 对每个未处理的项目集,计算其通过所有符号的转移,得到新的项目集,直到所有项目集都处理完毕。
4. FIRST和FOLLOW集合
4.1 FIRST集合
计算每个非终结符和终结符的FIRST集合。
- 对终结符,其FIRST集合是其本身。
- 对非终结符,通过递归计算其产生式右部的FIRST集合,考虑空字
LAMBDA。
4.2 FOLLOW集合
计算每个非终结符的FOLLOW集合,用于规约时确定接下来的符号。
- 起始符号的FOLLOW集合包含
EOF。 - 对每个产生式的右部,更新后续符号的FOLLOW集合,直到集合不再变化。
5. 构建分析表
5.1 动作表 (action_table)
用于存储移入、规约、接受等操作。
- 对于每个项目集中的项目,如果是移入项目,添加移入操作。
- 如果是规约项目,添加规约操作。
- 特殊处理接受项目,添加接受操作。
5.2 Goto表 (goto_table)
用于存储状态间的转移关系。
- 对于每个项目集和每个符号,记录其转移后的项目集。
6. 语法分析过程
6.1 分析过程
通过移入和规约操作,对输入的令牌序列进行分析,输出分析结果。
- 使用栈维护当前状态。
- 根据当前状态和输入符号,从动作表中查找相应操作。
- 移入操作:将符号移入栈,并转移到下一个状态。
- 规约操作:根据产生式进行规约,弹出符号并转移到下一个状态。
- 接受操作:成功匹配输入序列,结束分析。
- 错误处理:遇到无法处理的输入,报告错误。
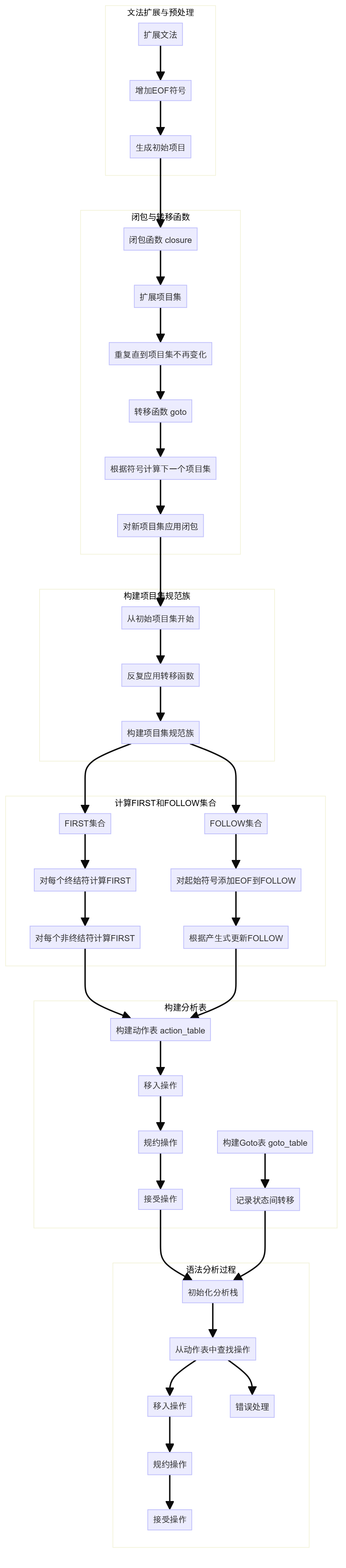
算法流程
SLR(1)分析程序为了实现对输入令牌序列的有效解析,能够判断输入是否符合给定的文法规则。
整个流程可以分为六步
- 文法扩展
- 闭包与转移函数
- 项目集规范族构建
- FIRST和FOLLOW集合计算
- 分析表构建
- 语法分析过程
1. 文法扩展与预处理
-
扩展文法:
- 增加一个新的开始符号
FAKE_S和相应的产生式FAKE_S -> 原始起始符号。 - 在终结符集合中添加特殊符号
EOF表示输入结束。
def grammar_with_fake_start(grammar): (prev_q0, vn, vt, prods) = deepcopy(grammar) q0 = FAKE_S vn.insert(0, q0) vt.append(EOF) prods.insert(0, (q0, [prev_q0])) return (q0, vn, vt, prods) - 增加一个新的开始符号
2. 闭包与转移函数
- 闭包函数 (closure):
- 对给定项目集,添加所有可能的后续项目,直到不再有新的项目加入为止。
def closure(items, grammar): (q0, vn, vt, prods) = grammar clo = items while True: new_items = set([]) for item in clo: stacktop = item_to_stacktop(item, grammar) if stacktop != None and stacktop not in vn: continue for prod_index, (head, body) in get_prods_with_head(stacktop, grammar): new_item = (prod_index, 0) new_items.add(new_item) if new_items <= clo: break else: clo = clo.union(new_items) return frozenset(clo) - 转移函数 (goto):
- 计算从一个项目集经过某个符号转移后到达的下一个项目集。
def goto(cc_i, symbol, grammar): (q0, vn, vt, prods) = grammar items = set([]) for item in cc_i: stacktop = item_to_stacktop(item, grammar) if symbol == stacktop: new_item = (item[0], item[1] + 1) items.add(new_item) return closure(items, grammar)
3. 构建项目集规范族
- 项目集规范族:
- 从初始项目集开始,反复应用转移函数,构建整个项目集规范族。
def canonical_collection(grammar): (q0, vn, vt, prods) = grammar grammar_symbols = vn + vt goto_table = {} q0_item = (0, 0) cc0 = closure(set([q0_item]), grammar) cc = set([cc0]) done = set([]) while True: new_ccs = set([]) for cc_i in cc: if cc_i in done: continue for symbol in grammar_symbols: cc_next = goto(cc_i, symbol, grammar) if len(cc_next) > 0 : new_ccs.add(cc_next) goto_table[(cc_i, symbol)] = cc_next done.add(cc_i) if new_ccs <= cc: break else: cc = cc.union(new_ccs) return (cc0, cc, goto_table)
4. FIRST和FOLLOW集合
- 计算FIRST集合:
- 对每个非终结符和终结符计算其FIRST集合。
def first(grammar): (q0, vn, vt, prods) = grammar first_table = {} first_table_snapshot = {} for t in vt: first_table[t] = set([t]) for nt in vn: first_table[nt] = set([]) while first_table != first_table_snapshot: first_table_snapshot = deepcopy(first_table) for head, body in prods: rhs = set([]) for i, b in enumerate(body): if i == 0 or LAMBDA in first_table[body[i - 1]]: if i == len(body) - 1: rhs = rhs.union(first_table[b]) else: rhs = rhs.union(first_table[b] - set([LAMBDA])) first_table[head] = first_table[head].union(rhs) return first_table - 计算FOLLOW集合:
- 对每个非终结符计算其FOLLOW集合,用于在规约时确定接下来的符号。
def follow(grammar, first_table): (q0, vn, vt, prods) = grammar follow_table = {} follow_table_snapshot = {} for nt in vn: follow_table[nt] = set([]) follow_table[q0] = set([EOF]) while follow_table != follow_table_snapshot: follow_table_snapshot = deepcopy(follow_table) for head, body in prods: trailer = follow_table[head] for b in reversed(body): if b in vt: trailer = set([b]) else: follow_table[b] = follow_table[b].union(trailer) if LAMBDA in first_table[b]: trailer = trailer.union(first_table[b] - set([LAMBDA])) else: trailer = first_table[b] return follow_table
5. 构建分析表
- 构建动作表 (action_table) 和 Goto表 (goto_table):
- 动作表用于存储移入、规约、接受等操作。
- Goto表用于存储状态间的转移。
def build_action_table(cc, goto_table, follow_table, grammar): (_, _, vt, _) = grammar action_table = {} for cc_i in cc: for item in cc_i: stacktop = item_to_stacktop(item, grammar) if not (item_is_complete(item, grammar) or stacktop in vt): continue head, body = item_to_prod(item, grammar) if head == FAKE_S: action_table.setdefault((cc_i, EOF), []).append((ACCEPT,)) elif item_is_complete(item, grammar): for a in follow_table[head]: action_table.setdefault((cc_i, a), []).append((REDUCE, item[0])) else: next_state = goto_table.get((cc_i, stacktop)) action_table.setdefault((cc_i, stacktop), []).append((SHIFT, next_state)) return action_table
6. 语法分析过程
- 分析输入串:
- 使用栈维护当前状态,根据当前状态和输入符号,从动作表中查找相应操作,并执行移入、规约或接受操作。
def parse(grammar, tokens): grammar = grammar_with_fake_start(grammar) cc0, cc, goto_table = canonical_collection(grammar) first_table = first(grammar) follow_table = follow(grammar, first_table) action_table = build_action_table(cc, goto_table, follow_table, grammar) stack = [cc0] token_index = 0 ok = True iter = 0 while True: iter += 1 token = tokens[token_index] stacktop_state = stack[-1] actions = action_table.get((stacktop_state, token[0])) if actions == None or len(actions) == 0: return (False, "No actions") if len(actions) > 1: print("Conflicts in the action table") action = actions[0] action_str = action[0] if len(action) == 2: if action[0] == "shift": action_str += " {0}".format(action[1]) else: action_str += " {0}".format(action[1]) if action[0] == SHIFT: next_state = action[1] stack.append(next_state) token_index += 1 elif action[0] == REDUCE: prod_index= action[1] prods = grammar[3] (head, body) = prods[prod_index] for _ in range(len(body)): stack.pop() stacktop_state = stack[-1] next_state = goto_table.get((stacktop_state, head), "DEFAULT2") stack.append(next_state) elif action[0] == ACCEPT: break else: ok = False break return (ok,)
源程序
代码分为两个程序:
- 主程序
- 测试程序(单元测试)(由于程序的功能比较复杂,在写的过程就需要进行测试,一部分一部分的测试,这样汇总起来才不会有什么bug难找到。)
- 主程序
from copy import deepcopy
# 定义一些常量
FAKE_S = "FAKE_S" # 假的开始符号
EOF = "EOF" # 输入结束符
SHIFT = "shift" # 移进操作
REDUCE = "reduce" # 规约操作
ACCEPT = "accept" # 接受操作
LAMBDA = "lambda" # 空字
# 增广文法:为文法增加一个假的开始符号和结束符
def grammar_with_fake_start(grammar):
(prev_q0, vn, vt, prods) = deepcopy(grammar)
q0 = FAKE_S
vn.insert(0, q0) # 将假开始符号加入非终结符集合
vt.append(EOF) # 将结束符加入终结符集合
prods.insert(0, (q0, [prev_q0])) # 增加新的产生式:FAKE_S -> 原始起始符号
return (q0, vn, vt, prods)
# 构建规范LR(1)项目集族
def canonical_collection(grammar):
(q0, vn, vt, prods) = grammar
grammar_symbols = vn + vt # 文法符号 = 非终结符 + 终结符
goto_table = {}
q0_item = (0, 0) # 初始项目
cc0 = closure(set([q0_item]), grammar) # 求初始项目的闭包
cc = set([cc0])
done = set([]) # 已处理的项目集
while True:
new_ccs = set([])
for cc_i in cc:
if cc_i in done:
continue
for symbol in grammar_symbols:
cc_next = goto(cc_i, symbol, grammar) # 计算转移
if len(cc_next) > 0 :
new_ccs.add(cc_next)
goto_table[(cc_i, symbol)] = cc_next
done.add(cc_i)
if new_ccs <= cc: # 如果没有新的项目集,跳出循环
break
else:
cc = cc.union(new_ccs) # 合并新的项目集
return (cc0, cc, goto_table)
# 闭包函数:对一个项目集进行闭包操作
def closure(items, grammar):
(q0, vn, vt, prods) = grammar
clo = items
while True:
new_items = set([])
for item in clo:
stacktop = item_to_stacktop(item, grammar)
if stacktop != None and stacktop not in vn:
continue
for prod_index, (head, body) in get_prods_with_head(stacktop, grammar):
new_item = (prod_index, 0)
new_items.add(new_item)
if new_items <= clo:
break
else:
clo = clo.union(new_items)
return frozenset(clo)
# 转移函数:计算从一个项目集经过某个符号转移后得到的项目集
def goto(cc_i, symbol, grammar):
(q0, vn, vt, prods) = grammar
items = set([])
for item in cc_i:
stacktop = item_to_stacktop(item, grammar)
if symbol == stacktop:
new_item = (item[0], item[1] + 1)
items.add(new_item)
return closure(items, grammar)
# 构建分析表
def build_action_table(cc, goto_table, follow_table, grammar):
(_, _, vt, _) = grammar
action_table = {}
for cc_i in cc:
for item in cc_i:
stacktop = item_to_stacktop(item, grammar)
if not (item_is_complete(item, grammar) or stacktop in vt):
continue
head, body = item_to_prod(item, grammar)
if head == FAKE_S:
action_table.setdefault((cc_i, EOF), []).append((ACCEPT,))
elif item_is_complete(item, grammar):
for a in follow_table[head]:
action_table.setdefault((cc_i, a), []).append((REDUCE, item[0]))
else:
next_state = goto_table.get((cc_i, stacktop))
action_table.setdefault((cc_i, stacktop), []).append((SHIFT, next_state))
return action_table
# 计算FIRST集合
def first(grammar):
(q0, vn, vt, prods) = grammar
first_table = {}
first_table_snapshot = {}
for t in vt:
first_table[t] = set([t])
for nt in vn:
first_table[nt] = set([])
while first_table != first_table_snapshot:
first_table_snapshot = deepcopy(first_table)
for head, body in prods:
rhs = set([])
for i, b in enumerate(body):
if i == 0 or LAMBDA in first_table[body[i - 1]]:
if i == len(body) - 1:
rhs = rhs.union(first_table[b])
else:
rhs = rhs.union(first_table[b] - set([LAMBDA]))
first_table[head] = first_table[head].union(rhs)
return first_table
# 计算FOLLOW集合
def follow(grammar, first_table):
(q0, vn, vt, prods) = grammar
follow_table = {}
follow_table_snapshot = {}
for nt in vn:
follow_table[nt] = set([])
follow_table[q0] = set([EOF])
while follow_table != follow_table_snapshot:
follow_table_snapshot = deepcopy(follow_table)
for head, body in prods:
trailer = follow_table[head]
for b in reversed(body):
if b in vt:
trailer = set([b])
else:
follow_table[b] = follow_table[b].union(trailer)
if LAMBDA in first_table[b]:
trailer = trailer.union(first_table[b] - set([LAMBDA]))
else:
trailer = first_table[b]
return follow_table
# 解析输入串
def parse(grammar, tokens):
print()
print("++++++++++++++++++++++++")
print("++++++++++++++++++++++++")
print("PARSE: {0}".format(tokens))
print("++++++++++++++++++++++++")
print("++++++++++++++++++++++++")
grammar = grammar_with_fake_start(grammar)
cc0, cc, goto_table = canonical_collection(grammar)
first_table = first(grammar)
follow_table = follow(grammar, first_table)
action_table = build_action_table(cc, goto_table, follow_table, grammar)
print_action_table(action_table, cc, grammar)
stack = [cc0]
token_index = 0
ok = True
iter = 0
while True:
print("")
print("============")
print("ITER: {0}".format(iter))
print("============")
iter += 1
print_stack(stack, cc)
token = tokens[token_index]
print("Token: {0}".format(token[0]))
stacktop_state = stack[-1]
actions = action_table.get((stacktop_state, token[0]))
if actions == None or len(actions) == 0:
return (False, "No actions")
if len(actions) > 1:
print("Conflicts in the action table")
action = actions[0]
action_str = action[0]
if len(action) == 2:
if action[0] == "shift":
action_str += " {0}".format(action[1])
else:
action_str += " {0}".format(action[1])
print("Action: {0}".format(action_str))
if action[0] == SHIFT:
next_state = action[1]
stack.append(next_state)
token_index += 1
elif action[0] == REDUCE:
prod_index= action[1]
prods = grammar[3]
(head, body) = prods[prod_index]
for _ in range(len(body)):
stack.pop()
stacktop_state = stack[-1]
next_state = goto_table.get((stacktop_state, head), "DEFAULT2")
stack.append(next_state)
print("reducing by {0} -> {1}".format(head, body))
elif action[0] == ACCEPT:
break
else:
print("ERROR")
print_stack(stack, cc, True)
ok = False
break
return (ok,)
##################
# 辅助函数
###################
# 获取项目的栈顶符号
def item_to_stacktop(item, grammar):
(_, _, _, prods) = grammar
(prod_index, stacktop_index) = item
(head, body) = prods[prod_index]
if stacktop_index >= len(body):
# 完成的项目
return None
else:
return body[stacktop_index]
# 获取项目对应的产生式
def item_to_prod(item, grammar):
(_, _, _, prods) = grammar
(prod_index, _) = item
return prods[prod_index]
# 判断项目是否完成
def item_is_complete(item, grammar):
return item_to_stacktop(item, grammar) == None
# 根据产生式头部获取产生式列表
def get_prods_with_head(desired_head, grammar):
if desired_head == None:
return []
(_, _, _, prods) = grammar
result = []
for prod_index, (current_head, body) in enumerate(prods):
if current_head != desired_head:
continue
result.append((prod_index, (current_head, body)))
return result
# 打印goto表
def print_goto_table(goto_table, cc):
id_map = {}
cc_list = list(cc)
print("INDEX")
for i, cc_i in enumerate(cc_list):
id_map[cc_i] = i
print("{0} -> {1}".format(i, cc_i))
print("GOTO")
for key, next_state in goto_table.iteritems():
state, symbol = key
print("{0:<10} {1:<10} -> {2}".format(id_map.get(state), symbol, id_map.get(next_state)))
# 打印action表
def print_action_table(action_table, cc, grammar):
id_map = {}
cc_list = list(cc)
print("INDEX")
for i, cc_i in enumerate(cc_list):
id_map[cc_i] = i
print("{0} -> {1}".format(i, cc_i))
print("ACTION")
for key, actions in action_table.items():
state, symbol = key
action_str = []
for action in actions:
if action[0] == ACCEPT:
action_str.append("ACCEPT")
elif action[0] == REDUCE:
action_str.append("Reduce {0}".format(prod_to_string(grammar[3][action[1]])))
elif action[0] == SHIFT:
action_str.append("Shift {0}".format(id_map.get(action[1])))
print("{0:<10} {1:<10} -> {2}".format(id_map.get(state), symbol, "".join(action_str)))
# 打印栈内容
def print_stack(stack, cc, index=False):
id_map = {}
cc_list = list(cc)
if index:
print("INDEX")
for i, cc_i in enumerate(cc_list):
id_map[cc_i] = i
if index:
print("{0} -> {1}".format(i, cc_i))
print("STACK: {0}".format(" ".join(map(lambda x: "{0}".format(id_map.get(x)), stack))))
print("=======")
print(" ".join(map(lambda x: "{0}".format(id_map.get(x)), stack)))
for state in reversed(stack):
print("{0}".format(id_map.get(state)))
print(state)
print("=======")
# 将产生式转换为字符串
def prod_to_string(prod):
head, body = prod
return "{0} -> {1}".format(head, " ".join(body))
# 主函数
if __name__ == '__main__':
prods = [
("E", ["E", "+", "T"]),
("E", ["T"]),
("T", ["T", "*", "F"]),
("T", ["F"]),
("F", ["(", "E", ")"]),
("F", ["id"]),
]
q0 = "E"
vn = ["E", "T", "F"]
vt = ["+", "*", "(", ")", "id"]
lines = []
tokens = []
while True:
try:
line = input()
if line == "":
break
lines.append(line)
except EOFError:
break
for line in lines:
type = line[1:line.index(",")]
if type == "lparen":
tokens.append("(")
elif type == "rparen" :
tokens.append(")")
elif type == "ident" or type == "number":
tokens.append("id")
elif type == "plus":
tokens.append("+")
elif type == "times" :
tokens.append("*")
else :
print("Error")
break
tokens = [(element,) for element in tokens] + [(EOF,)]
grammar = (q0, vn, vt, prods)
if(parse(grammar, tokens)[0]):
print("Yes,it is correct.")
else:
print("No,it is wrong.")
- 测试程序
import unittest
from main import *
prods = [
("E", ["E", "+", "T"]),
("E", ["T"]),
("T", ["T", "*", "F"]),
("T", ["F"]),
("F", ["(", "E", ")"]),
("F", ["id"]),
]
q0 = "E"
vn = ["E", "T", "F"]
vt = ["+", "*", "(", ")", "id"]
grammar = (q0, vn, vt, prods)
class Test(unittest.TestCase):
def test_grammar_with_fake_start(self):
grammar_ext = grammar_with_fake_start(grammar)
expected = (
FAKE_S,
[FAKE_S, "E", "T", "F"],
["+", "*", "(", ")", "id", EOF],
[
(FAKE_S, ["E"]),
("E", ["E", "+", "T"]),
("E", ["T"]),
("T", ["T", "*", "F"]),
("T", ["F"]),
("F", ["(", "E", ")"]),
("F", ["id"]),
]
)
self.assertEqual(grammar_ext, expected)
def test_closure(self):
items = closure(set([(0, 0)]), grammar)
expected = frozenset([
(0, 0),
(1, 0),
(2, 0),
(3, 0),
(4, 0),
(5, 0)
])
self.assertEqual(items, expected)
def test_goto(self):
cc0 = closure(set([(0, 0)]), grammar)
cc_i = goto(cc0, "E", grammar)
expected = frozenset([
(0, 1),
])
self.assertEqual(cc_i, expected)
def test_first(self):
(q0, vn, vt, prods) = grammar
first_table = first(grammar)
for t in vt:
self.assertEqual(first_table[t], set([t]))
self.assertEqual(first_table["E"], set(["(", "id"]))
self.assertEqual(first_table["T"], set(["(", "id"]))
self.assertEqual(first_table["F"], set(["(", "id"]))
def test_follow(self):
(q0, vn, vt, prods) = grammar
first_table = first(grammar)
follow_table = follow(grammar, first_table)
self.assertEqual(follow_table["E"], set([EOF, "+", ")"]))
self.assertEqual(follow_table["T"], set([EOF, "+", "*", ")"]))
self.assertEqual(follow_table["F"], set([EOF, "+", "*", ")"]))
def test_parse(self):
ok = parse(grammar, [("id", ), ("+", ), ("id",), (EOF, )])
self.assertTrue(ok)
ok = parse(grammar, [("id", ), (EOF, )])
self.assertTrue(ok)
ok = parse(grammar, [ (EOF, )])
self.assertTrue(ok)
def test_canonical_collection(self):
q0, cc, goto_table = canonical_collection(grammar)
self.assertEqual(q0, frozenset([
(0, 0),
(1, 0),
(2, 0),
(3, 0),
(4, 0),
(5, 0)
]))
self.assertEqual(
cc,
set([
frozenset([(2, 3)]),
frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 0),
]),
frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 1),
(4, 0),
]),
frozenset([(0, 1)]),
frozenset([(0, 1), (4, 2)]),
frozenset([(1, 1), (2, 1)]),
frozenset([(2, 2), (5, 0), (4, 0)]),
frozenset([(3, 0), (2, 0), (0, 2), (5, 0), (4, 0)]),
frozenset([(3, 1)]),
frozenset([(5, 1)]),
frozenset([(4, 3)]),
frozenset([(0, 3), (2, 1)]),
])
)
self.assertEqual(
goto_table,
{
(frozenset([(0, 1)]), '+'): frozenset([(3, 0), (2, 0), (0, 2), (5,
0), (4, 0)]),
(frozenset([(3, 0), (2, 0), (0, 2), (5, 0), (4, 0)]), 'id'
): frozenset([(5, 1)]),
(frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 0),
]), 'E'): frozenset([(0, 1)]),
(frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 1),
(4, 0),
]), '('): frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 1),
(4, 0),
]),
(frozenset([(2, 2), (5, 0), (4, 0)]), 'id'): frozenset([(5, 1)]),
(frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 0),
]), 'T'): frozenset([(1, 1), (2, 1)]),
(frozenset([(3, 0), (2, 0), (0, 2), (5, 0), (4, 0)]), 'T'
): frozenset([(0, 3), (2, 1)]),
(frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 0),
]), 'F'): frozenset([(3, 1)]),
(frozenset([(0, 1), (4, 2)]), ')'): frozenset([(4, 3)]),
(frozenset([(3, 0), (2, 0), (0, 2), (5, 0), (4, 0)]), 'F'
): frozenset([(3, 1)]),
(frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 1),
(4, 0),
]), 'E'): frozenset([(0, 1), (4, 2)]),
(frozenset([(3, 0), (2, 0), (0, 2), (5, 0), (4, 0)]), '('
): frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 1),
(4, 0),
]),
(frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 0),
]), '('): frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 1),
(4, 0),
]),
(frozenset([(0, 3), (2, 1)]), '*'): frozenset([(2, 2), (5, 0), (4,
0)]),
(frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 1),
(4, 0),
]), 'T'): frozenset([(1, 1), (2, 1)]),
(frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 0),
]), 'id'): frozenset([(5, 1)]),
(frozenset([(2, 2), (5, 0), (4, 0)]), '('): frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 1),
(4, 0),
]),
(frozenset([(2, 2), (5, 0), (4, 0)]), 'F'): frozenset([(2, 3)]),
(frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 1),
(4, 0),
]), 'F'): frozenset([(3, 1)]),
(frozenset([(1, 1), (2, 1)]), '*'): frozenset([(2, 2), (5, 0), (4,
0)]),
(frozenset([(0, 1), (4, 2)]), '+'): frozenset([(3, 0), (2, 0), (0,
2), (5, 0), (4, 0)]),
(frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(4, 1),
(4, 0),
]), 'id'): frozenset([(5, 1)]),
}
)
def test_build_action_table(self):
grammar_ext = grammar_with_fake_start(grammar)
cc0, cc, goto_table = canonical_collection(grammar_ext)
first_table = first(grammar_ext)
follow_table = follow(grammar_ext, first_table)
action_table = build_action_table(cc, goto_table, follow_table, grammar_ext)
print_action_table(action_table, cc, grammar_ext)
self.assertEqual(
action_table,
{
(frozenset([(4, 1)]), ')'): [('reduce', 4)],
(frozenset([(5, 3)]), '*'): [('reduce', 5)],
(frozenset([(1, 2), (3, 0), (6, 0), (5, 0), (4, 0)]), 'id'
): [('shift', frozenset([(6, 1)]))],
(frozenset([(5, 2), (1, 1)]), '+'): [('shift', frozenset([(1, 2),
(3, 0), (6, 0), (5, 0), (4, 0)]))],
(frozenset([(0, 1), (1, 1)]), 'EOF'): [('accept', )],
(frozenset([(3, 3)]), ')'): [('reduce', 3)],
(frozenset([(3, 2), (6, 0), (5, 0)]), 'id'): [('shift',
frozenset([(6, 1)]))],
(frozenset([(3, 1), (2, 1)]), '+'): [('reduce', 2)],
(frozenset([(1, 3), (3, 1)]), '*'): [('shift', frozenset([(3, 2),
(6, 0), (5, 0)]))],
(frozenset([(5, 3)]), ')'): [('reduce', 5)],
(frozenset([(3, 3)]), 'EOF'): [('reduce', 3)],
(frozenset([(5, 3)]), '+'): [('reduce', 5)],
(frozenset([(6, 1)]), '+'): [('reduce', 6)],
(frozenset([(4, 1)]), 'EOF'): [('reduce', 4)],
(frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(6, 0),
(4, 0),
]), '('): [('shift', frozenset([
(2, 0),
(5, 0),
(3, 0),
(5, 1),
(1, 0),
(6, 0),
(4, 0),
]))],
(frozenset([(5, 3)]), 'EOF'): [('reduce', 5)],
(frozenset([(3, 3)]), '*'): [('reduce', 3)],
(frozenset([(1, 3), (3, 1)]), ')'): [('reduce', 1)],
(frozenset([(3, 2), (6, 0), (5, 0)]), '('): [('shift', frozenset([
(2, 0),
(5, 0),
(3, 0),
(5, 1),
(1, 0),
(6, 0),
(4, 0),
]))],
(frozenset([(0, 1), (1, 1)]), '+'): [('shift', frozenset([(1, 2),
(3, 0), (6, 0), (5, 0), (4, 0)]))],
(frozenset([(6, 1)]), '*'): [('reduce', 6)],
(frozenset([(4, 1)]), '+'): [('reduce', 4)],
(frozenset([(6, 1)]), 'EOF'): [('reduce', 6)],
(frozenset([(3, 3)]), '+'): [('reduce', 3)],
(frozenset([(1, 3), (3, 1)]), 'EOF'): [('reduce', 1)],
(frozenset([(3, 1), (2, 1)]), 'EOF'): [('reduce', 2)],
(frozenset([(5, 2), (1, 1)]), ')'): [('shift', frozenset([(5,
3)]))],
(frozenset([
(2, 0),
(5, 0),
(3, 0),
(5, 1),
(1, 0),
(6, 0),
(4, 0),
]), '('): [('shift', frozenset([
(2, 0),
(5, 0),
(3, 0),
(5, 1),
(1, 0),
(6, 0),
(4, 0),
]))],
(frozenset([(3, 1), (2, 1)]), ')'): [('reduce', 2)],
(frozenset([(4, 1)]), '*'): [('reduce', 4)],
(frozenset([(6, 1)]), ')'): [('reduce', 6)],
(frozenset([
(2, 0),
(0, 0),
(5, 0),
(3, 0),
(1, 0),
(6, 0),
(4, 0),
]), 'id'): [('shift', frozenset([(6, 1)]))],
(frozenset([(1, 2), (3, 0), (6, 0), (5, 0), (4, 0)]), '('
): [('shift', frozenset([
(2, 0),
(5, 0),
(3, 0),
(5, 1),
(1, 0),
(6, 0),
(4, 0),
]))],
(frozenset([(3, 1), (2, 1)]), '*'): [('shift', frozenset([(3, 2),
(6, 0), (5, 0)]))],
(frozenset([(1, 3), (3, 1)]), '+'): [('reduce', 1)],
(frozenset([
(2, 0),
(5, 0),
(3, 0),
(5, 1),
(1, 0),
(6, 0),
(4, 0),
]), 'id'): [('shift', frozenset([(6, 1)]))],
}
)
if __name__ == '__main__':
unittest.main()
调试数据
样例输入
(lparen,()
(ident,b)
(plus,+)
(number,9)
(rparen,))
(times,\*)
(ident,a)
样例输出
Yes,it is correct.
运行结果
- 分析产生action表的过程:
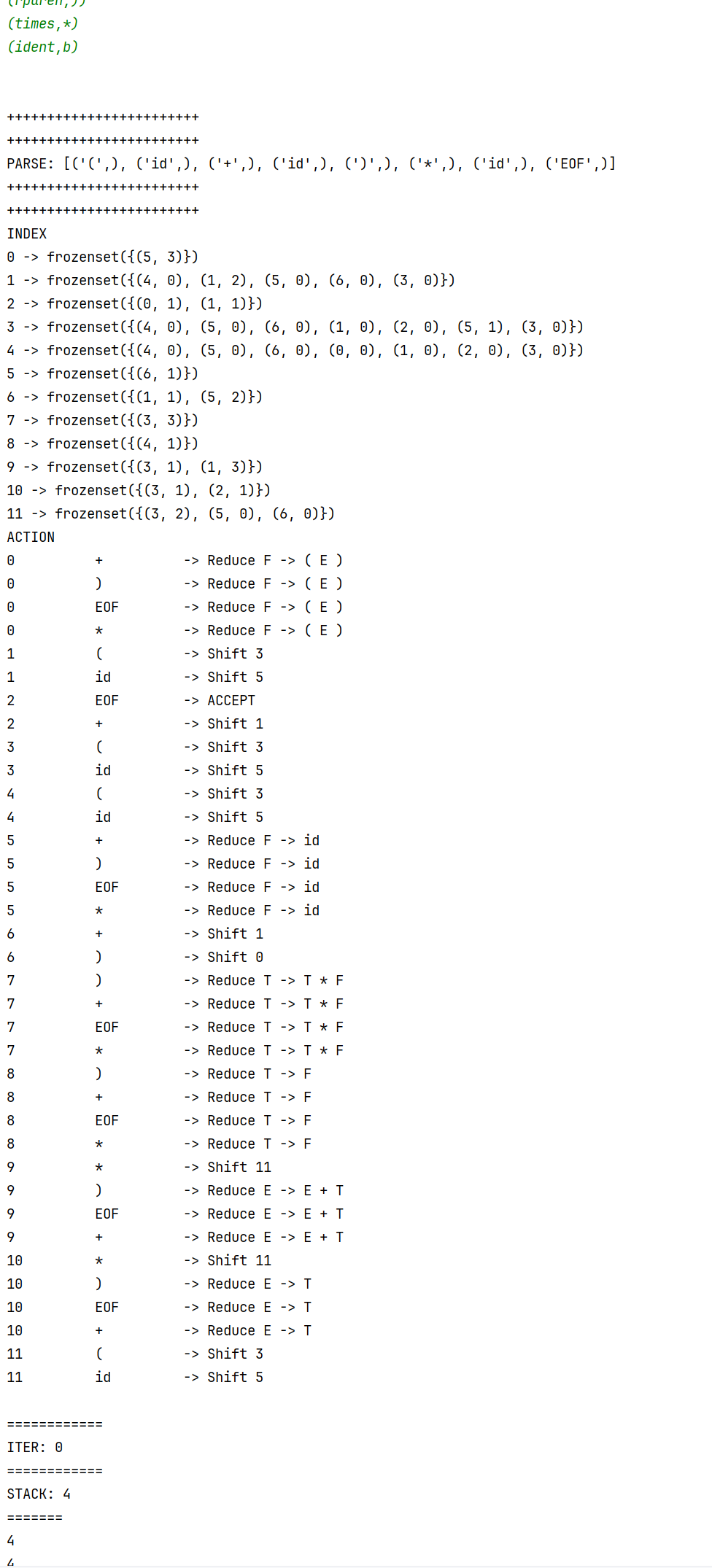
-
语法分析过程

实验调试情况及体会
在这次实验中,尽管题目仅仅要求编写一个分析程序,但我却主动挑战自己,完成了SLR(1)分析表的构建。这无疑加大了实验的难度,但也为我提供了难得的挑战和成长机会。选择使用SLR(1)文法进行分析,不仅需要考虑向前搜索符,更是对自己能力的一次全面考验。
本次实验得益于以前良好的编程习惯,每写一部分就调试一部分查看一部分的bug,这样总的程序虽然非常长,但是中间的bug都被一一排除了,然后就能够得出了正确的结果,还是非常的不容易,最终实现了SLR(1)的分析,并且适用于其他文法,可以自己输入产生式,然后进行分析。并且实验过程中,我一步步地完成实验各个环节。当设计尚未明确时,我了分阶段完成。首先生成一个状态的所有项目,然后考虑如何求该状态的转移,再进一步求转移后的状态。在这个过程中,逐步深化细节,例如如何判断两个状态集是否相同等问题。最终,我成功地求出了所有状态,并记录了状态转移情况。这样,编写分析表和分析程序的过程变得更加顺利。
这次实验带给我巨大的收获,与之前编写的LL(1)文法形成了鲜明对比。例如,在一开始编写时,我没有注意到左递归的消除问题,这让我在完成实验后对此问题印象更加深刻。通过这次实验,我对每一个过程和步骤都有了更深的理解。
这次实验不仅让我提升了技术能力,更让我体会到了从挑战中获得成长的喜悦。实验过程中的每一个小细节,都让我对编译原理有了更深入的理解。尽管实验过程充满挑战,但最终的成功让我感到无比的满足和自豪。感谢这次实验,让我在编程的道路上迈出了重要的一步,未来我将继续努力,不断提升自己的技能,迎接更多的挑战。