LoRA LOW-RANK ADAPTATION 论文笔记

不懂的问题

线性代数基础

根据线性代数的性质：

若 $B \in \mathbb{R}^{512 \times 4}$ 和 $A \in \mathbb{R}^{4 \times 512}$，则矩阵乘积 $\Delta W = B A$ 的最大秩 $\text{rank}(\Delta W)$ 由 $B$ 和 $A$ 的秩中较小的那个决定： $\text{rank}(\Delta W) \leq \min (\text{rank}(B), \text{rank}(A))$
在 LoRA 的低秩分解中：
- $B$ 的列数是 4，其秩最多为 4。
- $A$ 的行数是 4，其秩最多为 4。
- 因此，$\Delta W = B A$ 的秩最多为 4。
虽然 $\Delta W$ 的尺寸是 $512 \times 512$，但它的 列空间维度（rank） 被限制在 4，即列向量最多线性独立的维度是 4。

假设我们有一个 $512 \times 512$ 的矩阵更新：

如果直接更新 $\Delta W$ 的每个元素（完整微调），那么矩阵的秩可以达到最大值 512。
LoRA 的假设是任务适配过程中权重更新的本质维度较低，因此可以用 4 个基向量（来自 $B$ 的列空间） 和它们的线性组合来近似表示更新。

这意味着即使 $\Delta W$ 的尺寸是 $512 \times 512$，其独立的方向（秩）是受 $r = 4$ 的限制的。

所以这正是为什么通过调整 $r$ 可以控制 LoRA 的表达能力：$r$ 越大，权重更新的潜在方向越多，表达能力越强；当 $r$ 接近 512 时，LoRA 的表达能力接近完整微调。

摘要

问题

模型越来越大，全参数 SFT 变的不可行

作者的工作

LORA：该方法冻结预训练模型的权重，并将可训练的秩分解矩阵注入到Transformer架构的每一层，极大地减少了下游任务的可训练参数数量。

结果

与使用Adam微调的GPT-3 175B相比，LoRA可以将可训练参数的数量减少10,000倍，并将GPU内存需求减少3倍。
尽管可训练参数较少，训练吞吐量更高，并且与适配器不同，不会增加额外的推理延迟，LoRA在RoBERTa、DeBERTa、GPT-2和GPT-3的模型质量上表现与微调持平或更好

引言

问题：模型越来越大，全参数 SFT 变的不可行
现有解决方法：针对不同任务添加一些参数或者适配器
- 好处：只需要存储和加载少量的任务特定参数，除了每个任务的预训练模型外，极大地提高了部署时的操作效率。
- 缺点：适配器会增加推理了延迟、无法与达到微调基础，在效率和质量直接由权衡

LoRA

灵感：LoRA 的灵感来源于研究表明，过参数化的模型其实存在于一个低维空间。也就是说，在模型适应（fine-tuning）过程中，权重的变化可以用一个低秩结构表示（即低秩分解）。
核心思想：
- 冻结预训练模型权重：只优化特定层的“变化部分”。
- 低秩分解：通过优化某些密集层变化的低秩分解矩阵（如图中提到的矩阵 AAA 和 BBB），实现模型适应。
- 例如，GPT-3 175B 预训练模型中的一个矩阵，其原始秩（rank）为 12,288，LoRA 只需优化秩 r=1r=1r=1 或 r=2r=2r=2 的矩阵就能完成 fine-tuning。

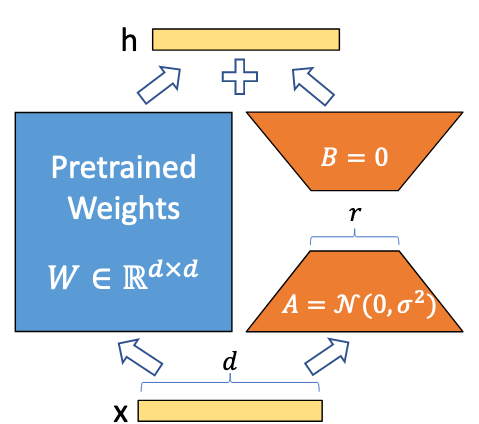
这张图是 LoRA（Low-Rank Adaptation） 方法的关键机制示意图，展示了如何对预训练模型中的权重矩阵 $W \in \mathbb{R}^{d \times d}$ 进行低秩分解和优化。

图中元素解释

Pretrained Weights $W$：
- $W$ 是预训练模型中的一个权重矩阵，其维度为 $d \times d$。
- 在 LoRA 方法中，这个矩阵 保持冻结（不更新）。
输入 $x$ 和输出 $h$：
- 输入 $x$ 是特征向量，其维度为 $d$。
- 输出 $h$ 是经过 LoRA 适配后的向量，作为网络的输出，维度同样为 $d$。
低秩分解矩阵 $A$ 和 $B$：
- LoRA 引入两个小规模的低秩矩阵 $A \in \mathbb{R}^{d \times r}$ 和 $B \in \mathbb{R}^{r \times d}$，其中 $r \ll d$（例如 $r=1$ 或 $r=2$）。
- $A$ 和 $B$ 的作用是近似描述 $W$ 的变化（即微调时需要的调整量 $\Delta W$）。
- 在初始化时：
  - $A$ 通常从高斯分布 $\mathcal{N}(0, \sigma^2)$ 中随机采样。
  - $B$ 初始化为零矩阵。
模型调整机制：
- 微调时，仅优化 $A$ 和 $B$ 的参数，而不改变 $W$。
- 输入 $x$ 经过计算后产生一个调整量： $\Delta h = B \cdot (A \cdot x)$
- 最终输出为： $H = W \cdot x + \Delta h$
- 这表明模型输出是预训练权重 $W$ 的结果加上一个低秩调整项。

LoRA 优势

共享和高效任务切换：
- 模块化：预训练模型可以用于多个任务。LoRA 通过替换不同的低秩矩阵 AAA 和 BBB，实现了高效的任务切换。
- 减少存储需求：因为只需要存储这些小的矩阵，而不是整个模型参数。
提高训练效率：
- 降低硬件门槛：相比传统方法，LoRA 只优化小规模矩阵，因此显著减少计算量。根据文中描述，可以将所需的硬件资源减少到原来的三分之一。
零推理延迟：
- LoRA 的设计可以在部署时将优化的矩阵与预训练权重合并，因此不会增加推理延迟。
方法的通用性和组合性：
- LoRA 独立于其他方法，如前缀微调（prefix-tuning），并且可以与这些方法组合使用以增强效果。

术语约定

关于 Transformer 的术语和维度
- $d_{\text{model}}$：
  - 表示 Transformer 模型中某一层的输入和输出向量的维度。
  - 在 Transformer 的每一层中，所有的输入和输出张量都会使用这个维度。
- 投影矩阵（Projection Matrices）：
  - $W_q$：用于生成 query（查询向量）的投影矩阵。
  - $W_k$：用于生成 key（键向量）的投影矩阵。
  - $W_v$：用于生成 value（值向量）的投影矩阵。
  - $W_o$：表示 输出投影矩阵。
  - 这些矩阵都位于 自注意力模块（self-attention module） 内，是 Transformer 的核心部分。

权重的定义
- $W$ 或 $W_0$：
  - 代表 Transformer 中某一层的 预训练权重矩阵，这些矩阵通过预训练模型获得，在微调时被冻结（即不被更新）。
- $\Delta W$：
  - 代表 LoRA 在微调过程中累计更新的权重变化量。
  - LoRA 的核心思想是通过优化这个权重变化量，而不是直接修改原始的权重矩阵 $W$。

LoRA 的秩（Rank）$r$
- $r$：
  - 表示 LoRA 中低秩分解矩阵的秩（rank）。
  - $r$ 通常远小于 $d_{\text{model}}$，用来表示矩阵分解的低维度，从而降低优化问题的计算复杂度。

优化方法和架构设置
- 优化方法：
  - 作者采用了 Adam 优化器，这是一个在深度学习中常用的自适应学习率优化算法（参考：Loshchilov & Hutter, 2019 和 Kingma & Ba, 2017）。
- MLP 维度设置：
  - Transformer 中多层感知机（MLP）的隐藏层维度定义为： $D_{\text{ffn}} = 4 \times d_{\text{model}}$
  - 意味着 MLP 的隐藏层通常比输入输出的维度大 4 倍，用于增强模型的非线性表达能力。

问题陈述

LoRA 不涉及 loss 的设计，而是专注于语言建模任务的优化方法

1. 背景：预训练模型

假设我们有一个预训练的自回归语言模型（autoregressive language model）： $P_\Phi (y|x)$ 其中： - $x$：输入序列（例如任务的 prompt 或上下文）。 - $y$：输出序列（例如模型生成的文本）。 - $\Phi$：模型参数。

被用于解决多种下游任务（downstream tasks），如文本摘要（summarization）、阅读理解（MRC）、自然语言到 SQL 转换（NL 2 SQL）等。
任务定义：
- 每个下游任务通过一个训练数据集表示： $\mathcal{Z} = \{(x_i, y_i)\}_{i=1}^N$ 其中 $x_i$ 是输入序列，$y_i$ 是目标序列（输出）。
  - 例如，在 NL 2 SQL 任务中：
    - $x_i$：自然语言查询。
    - $y_i$：对应的 SQL 命令。
  - 在摘要任务中：
    - $x_i$：文章内容。
    - $y_i$：文章摘要。

2. 完整微调（Full Fine-Tuning）的问题

在传统的完整微调方法中：
- 模型会从预训练权重 $\Phi_0$ 开始进行优化。
- 更新后的模型参数为： $\Phi = \Phi_0 + \Delta \Phi$ 其中 $\Delta \Phi$ 是模型在下游任务上的更新。
目标是最大化条件语言建模目标： $\max_{\Phi} \sum_{(x, y) \in \mathcal{Z}} \sum_{t=1}^{|y|} \log P_\Phi (y_t | x, y_{<t})$ 这里：
- $y_t$：序列的第 $t$ 个 token。
- $y_{<t}$：序列的前 $t-1$ 个 token。
主要问题：
1. 存储需求：
  - 对于每个下游任务，需要学习不同的参数 $\Delta \Phi$，其维度和 $\Phi_0$ 一样大。
  - 如果预训练模型很大（例如 GPT-3，参数量高达 175 亿），存储多个独立的模型实例变得非常困难甚至不可行。
2. 部署复杂性：
  - 部署和维护多个完整微调后的模型对存储和计算资源要求很高。

3. LoRA 的方法：参数高效微调

为了解决上述问题，LoRA 提出了一个 更高效的微调方法，核心是：
- 将任务特定的参数增量 $\Delta \Phi$ 编码为一个 低维参数集 $\Theta$，满足： $|\Theta| \ll |\Phi_0|$
- 这样，微调的任务变成了优化 $\Theta$： $\max_{\Theta} \sum_{(x, y) \in \mathcal{Z}} \sum_{t=1}^{|y|} \log P_{\Phi_0 + \Delta \Phi (\Theta)}(y_t | x, y_{<t})$
低秩表示的优点：
- 通过使用低秩分解（low-rank representation），可以显著减少存储和计算成本。
- 当模型是 GPT-3（175 B 参数量）时，$\Theta$ 的规模可以小到原始参数规模的 0.01%。

现有的方法

迁移学习的现有方法

转移学习的方法有很多，当前主流方法包括：
1. 适配器层（Adapter Layers）：通过在模型的 Transformer 层中插入小型适配器模块进行调整。
2. Prompt Tuning：通过优化输入提示（Prompt）来适配下游任务。
这些方法在参数和计算效率上取得了进展，但在 大规模生产环境 中仍存在明显缺点，例如增加推理延迟或优化难度。

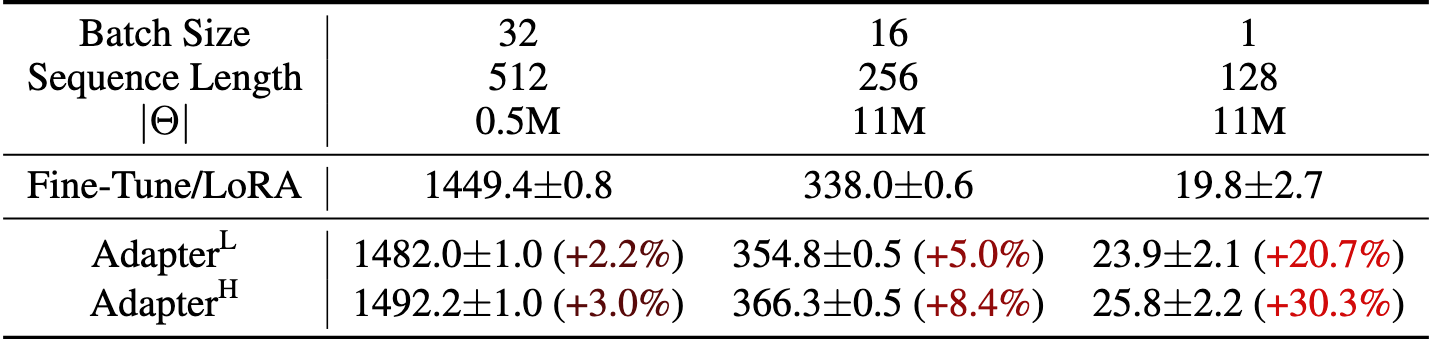
适配器层的不足：引入推理延迟

(1) 适配器层的设计：

原始适配器层设计（例如 Houlsby et al., 2019）在每个 Transformer 块中插入两层适配器。
后续方法（例如 Lin et al., 2020）优化了设计，减少为每块一层，并引入了额外的 LayerNorm，进一步降低了延迟。

(2) 延迟来源：

顺序处理的限制：适配器层尽管参数量很小（通常 <1% 的原始模型参数），但它们需要逐层顺序执行，限制了并行处理能力。
延迟问题明显：在在线推理（batch size 较小，例如 batch size = 1）中，由于缺乏并行性，适配器层显著增加了推理延迟。
分片（Sharding）的复杂性：在模型分片场景（如 Shoeybi et al., 2020）中，适配器层会增加更多 GPU 间的同步操作（如 AllReduce 和 Broadcast），进一步提高了开销。

(3) 表格中的数据说明：

表格展示了 GPT-2 模型在使用适配器层和其他方法时的推理延迟：
- Fine-Tune/LoRA 方法延迟最小（例如 batch size = 1 时仅 19.8 毫秒）。
- Adapter Layers 方法的延迟明显更高：
  - Adapter$L$ 和 Adapter$H$ 分别增加了 20.7% 和 30.3% 的延迟。
  - 延迟增加在小 batch size 场景尤为明显。

Prompt Tuning 的不足

(1) 优化难度：

Prompt Tuning 的优化过程较难，表现为：
- 随着可训练参数增加，性能的变化呈现 非单调性（即增加参数量并不一定提升性能）。
- 作者观察到这种现象在原始论文（Li & Liang, 2021）中也被证实。

(2) 序列长度限制：

Prompt Tuning 需要保留一部分序列作为 Prompt，这会减少可用于任务处理的序列长度，进而限制模型性能。
例如，原始输入序列长度可能被占用一部分用于 Prompt，从而减少了处理有效任务的空间。

(3) 性能潜力受限：

Prompt Tuning 在下游任务的表现可能不如其他方法，例如适配器层或 LoRA。

LoRA 方法

LoRA原则上适用于深度学习模型中的任何稠密层，尽管在我们的实验中我们只关注 Transformer 语言模型中的某些权重作为激励使用案例。

通过低秩分解（low-rank decomposition）来高效更新权重矩阵

1. 低秩参数化更新矩阵（Low-Rank-Parameterized Update Matrices）

神经网络的权重矩阵通常是全秩（full-rank）的。
LoRA 假设：预训练语言模型的权重更新可以被约束在一个 低秩子空间 中。
核心公式： $W_0 + \Delta W = W_0 + BA$
- $W_0 \in \mathbb{R}^{d \times k}$：预训练模型中的冻结权重矩阵。
- $\Delta W \in \mathbb{R}^{d \times k}$：权重的更新量。
- $B \in \mathbb{R}^{d \times r}, A \in \mathbb{R}^{r \times k}$：两个可训练的低秩矩阵，其中 $r \ll \min (d, k)$。
- 低秩分解的核心思想：通过约束 $\Delta W$ 为低秩表示，显著减少了优化参数量。
在训练过程中：
- $W_0$ 冻结，不会更新。
- $A$ 和 $B$ 是唯一需要优化的矩阵。
- 输入向量 $x$ 的前向计算公式变为： $H = W_0 x + \Delta Wx = W_0 x + BAx$

初始化和优化细节
- 初始化方式：
  - $A$ 的初始值来自随机高斯分布。
  - $B$ 的初始值为零矩阵。
  - 因此，$\Delta W = BA = 0$ 在训练开始时为零。

缩放机制
- $\Delta W$ 被缩放为： $\Delta W = \frac{\alpha}{r} BA$ 其中 $\alpha$ 是一个比例常数，与秩 $r$ 成反比。$\alpha$ 是缩放因子，用于调整更新幅度
- 调整 $\alpha$ 的作用类似于调整学习率，可以减少因 $r$ 变化导致的超参数重新调整需求。

这段话主要说明了 LoRA（Low-Rank Adaptation） 是完整微调（full fine-tuning）的一种泛化形式，并对其表达能力及与其他方法的对比做出分析。以下是详细解释：

3. 适用于所有全参数微调

完整微调的传统方式：
- 一般来说，完整微调会训练预训练模型中的 部分参数 或者 全部参数。
- 这些训练参数可以包括权重矩阵以及模型中的偏置（bias）。
LoRA 的突破：
- LoRA 提出了一种更通用的微调形式：
  - 不需要直接调整完整的权重矩阵（full-rank updates），而是通过低秩分解（low-rank decomposition）来表示权重更新。
  - 在应用 LoRA 时，对所有权重矩阵应用低秩更新，同时训练模型中的所有偏置项，可以近似恢复完整微调的表达能力
LoRA 的效果
- 效果主要取决于 LoRA 的秩 $r$：
  - LoRA 中的权重更新是通过两个低秩矩阵 $B$ 和 $A$ 表示的，秩 $r$ 决定了更新矩阵的表达能力。
  - 当 $r$ 增加并接近于原始权重矩阵的秩时，LoRA 的表达能力接近于完整微调。
与其他方法的对比
- 适配器层方法（adapter-based methods）：
  - 适配器方法在微调时，会插入额外的层进行任务适配。
  - 缺点：
    - 当增加可训练参数时，这些方法的表现最终会趋于类似于一个多层感知机（MLP），难以与完整微调匹敌。
- 基于前缀的微调方法（prefix-based methods）：
  - 例如 Prompt Tuning，通过优化前缀（prompt）来适配任务。
  - 缺点：
    - 受限于输入序列的长度（部分序列长度被前缀占用），在长输入序列的任务中表现不佳。
- LoRA 的优势：
  - 通过调整秩 $r$，LoRA 在模型训练参数的规模增加时，可以更接近完整微调的表现，同时不会受到序列长度或其他限制。

4. 推理时的零延迟（No Additional Inference Latency）

推理阶段的操作：
- 在生产部署中，可以直接计算并存储： $W = W_0 + BA$
- 推理时，模型直接使用 $W$ 进行计算，与原始全权重模型完全一致，无需额外计算。
切换任务：
- 当需要切换到其他任务时，只需移除现有的 $BA$，并替换为新的 $B’A’$，这一过程非常快且占用极少的内存。
- 这种特性特别适合需要频繁切换任务的应用场景。

将 LoRA 应用于 Transformer 模型

好处：

内存和存储的减少
- 内存的减少：VRAM 减少了 2/3 ，因为冻结的参数不需要为这些参数存储梯度和优化器状态，显存需求降低至原来的 1/3（1.2 TB -> 350 GB）
- 存储的减少：模型的保存文件减少了 10,000 倍（350 GB -> 35 MB）
切换任务代价更低：我们可以在部署时以更低的成本在任务之间切换，只需交换 LoRA 权重，而不是所有参数
训练速度也提高了 25%：因为不需要计算绝大多数参数的梯度。

缺点：

不同任务的批量处理不行

例如，如果选择将 A 和 B 吸收到 W 中以消除额外的推理延迟，那么在单次前向传播中，将不同任务的不同 A 和 B 批量输入并不是很简单。
尽管在延迟不关键的场景中，可以不合并权重，并动态选择批次中样本使用的 LoRA 模块。

实验

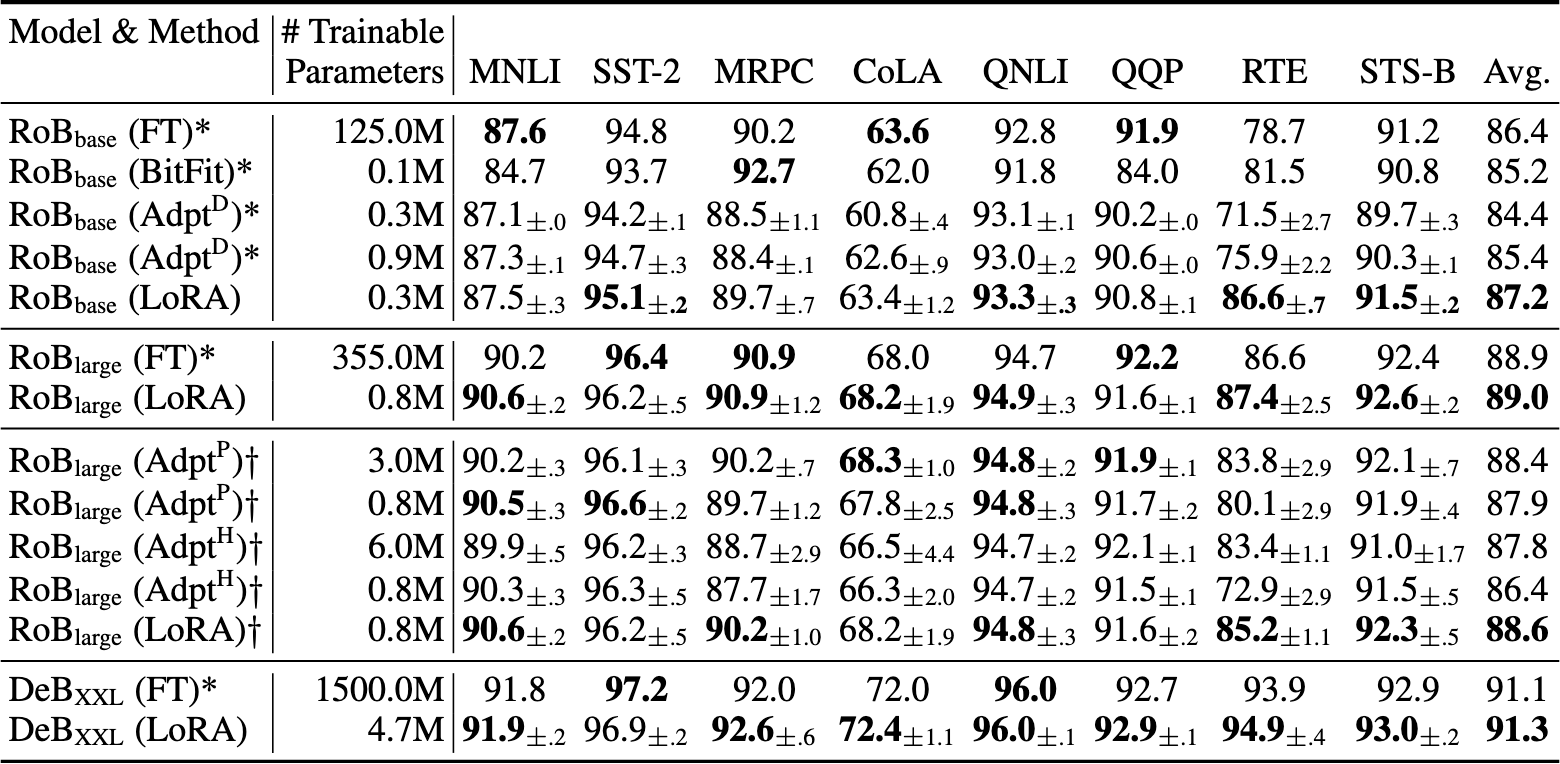
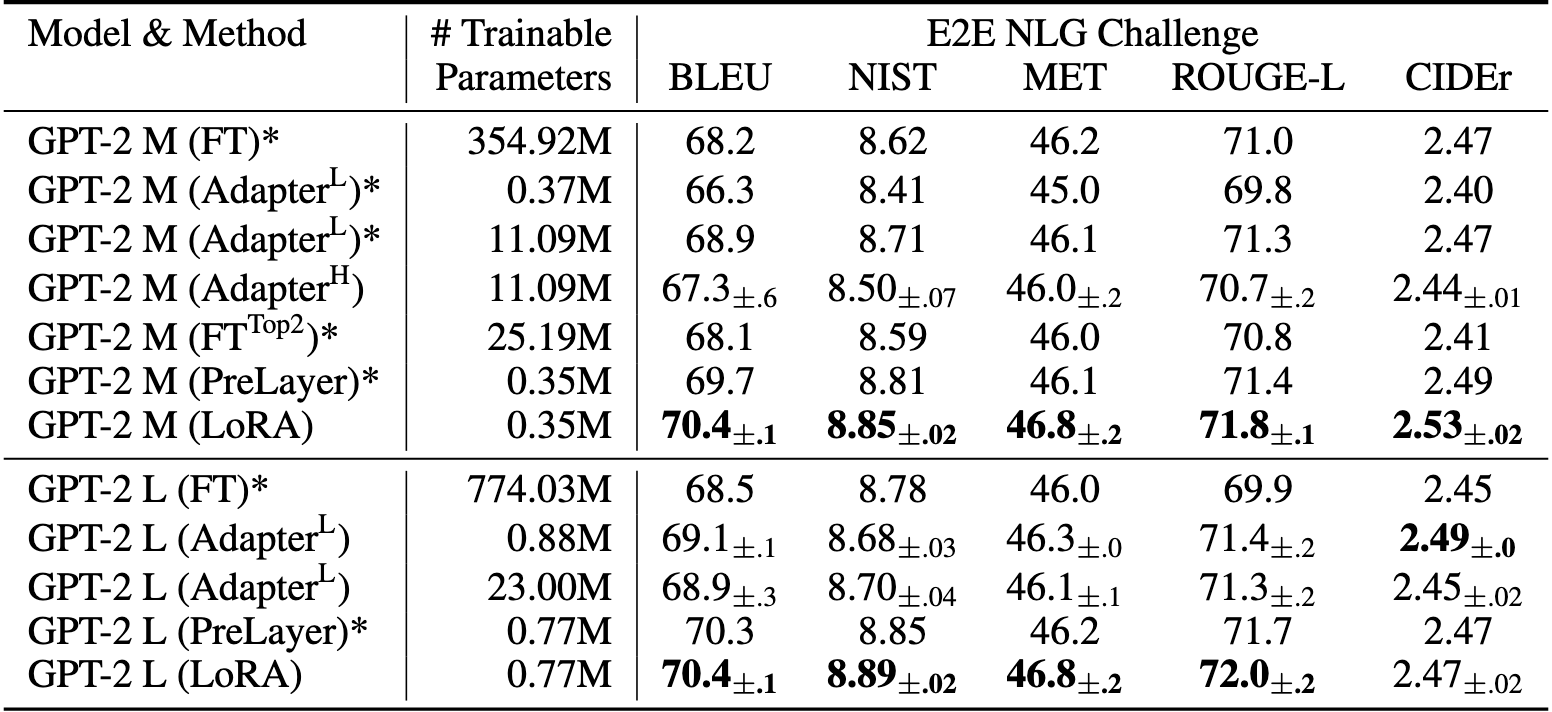
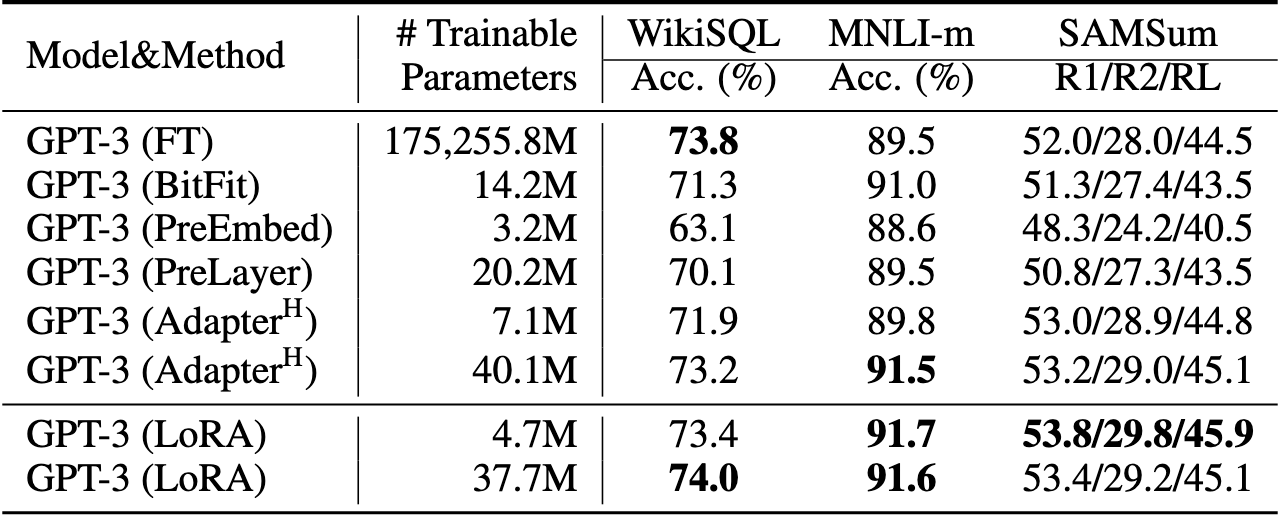
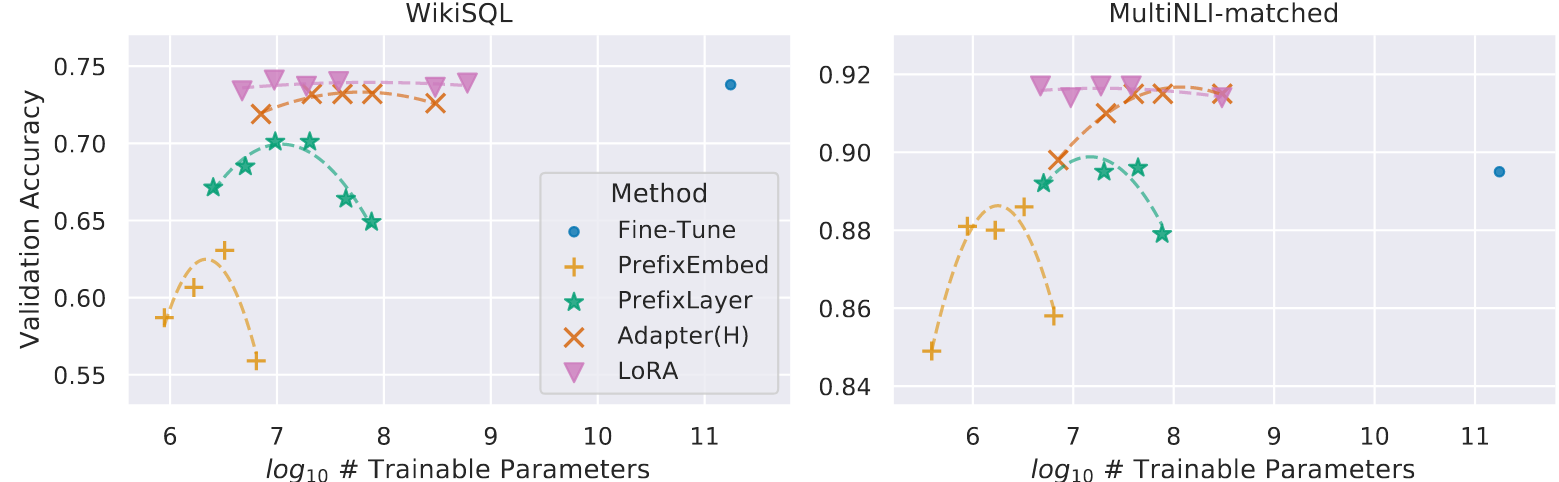GPT-3 175B 验证准确率与 WikiSQL 和 MNLI-matched 上多种适应方法的可训练参数数量。LoRA 展现了更好的可扩展性和任务性能。

理解 LoRA

要理解三个问题：

1) 在参数预算约束下，应该调整预训练 Transformer 中的哪一部分权重矩阵以最大化下游性能？ 2) “最优”调整矩阵∆W 真的是秩亏的吗？如果是，实际中使用哪个秩比较好？ 3) ∆W 与 W 之间有什么联系？∆W 是否与 W 高度相关？与 W 相比，∆W 有多大？

问题一：哪些权重应该调整？

这部分讨论了在参数预算有限的情况下，应该对 Transformer 中的哪些权重矩阵应用 LoRA，以在下游任务中获得最佳性能。以下是详细解释：

1. 研究目标

问题：在给定的参数预算（例如 18 M 可训练参数）下，如何选择 Transformer 模型中需要 LoRA 适配的权重矩阵类型，以获得最佳的任务性能。
背景：Transformer 的自注意力模块包含四种主要的权重矩阵：$W_q, W_k, W_v, W_o$。LoRA 可以单独适配某一个矩阵，也可以组合适配多个矩阵。
目标：探索不同权重组合的适配效果，并分析对验证集准确率的影响。

2. 实验设置

参数预算：
- 总的可训练参数设置为 18 M。
- 在存储为 FP 16 格式时，占用约 35 MB 的存储空间。
秩 $r$：
- 如果只适配一个矩阵，则 $r = 8$。
- 如果适配两个矩阵，则每个矩阵的 $r = 4$。
- 如果适配更多矩阵（例如四个矩阵），则 $r$ 会进一步降低，以满足总参数预算。
模型：
- 使用 GPT-3 175 B 作为基础模型。
- 在两个任务上验证效果：
  - WikiSQL（±0.5% 的标准差）：结构化查询的自然语言转换任务。
  - MultiNLI（±0.1% 的标准差）：文本蕴含任务。

3. 结论分析

单独适配某一种权重矩阵：
- 适配单个矩阵时，准确率相对较低，尤其是 $W_q$ 和 $W_k$ 单独适配的表现明显低于组合适配。
组合适配的优越性：
- 适配 $W_q$ 和 $W_v$ 的组合效果最佳。
- 这表明，即使每种矩阵的秩较低（如 $r = 4$），组合适配多个矩阵可以捕获更多的任务相关信息，从而比单独适配一个矩阵表现更好。
适配更多矩阵（如 $W_q, W_k, W_v, W_o$）：
- 在 MultiNLI 上，适配所有四个矩阵的表现达到最优（91.7%）。
- 说明在更复杂的任务中，适配更多权重矩阵（即使每个矩阵的秩更低）有助于提升模型的适配能力。

4. 结论

有效利用参数预算：
- 将参数预算分配给多个权重矩阵的适配，比将预算集中于单个矩阵更有效。
- 即使每个矩阵的秩较低，组合适配能更好地捕获任务所需的信息。
权重选择的重要性：
- $W_q$ 和 $W_v$ 的组合对性能提升尤为重要。
- 表明在 Transformer 中，不同权重矩阵对任务的影响不同，选择关键权重进行适配是提高性能的关键。
任务复杂性影响：
- 对于更复杂的任务（如 MultiNLI），适配更多权重矩阵效果更好。

问题二：最优秩是多少？

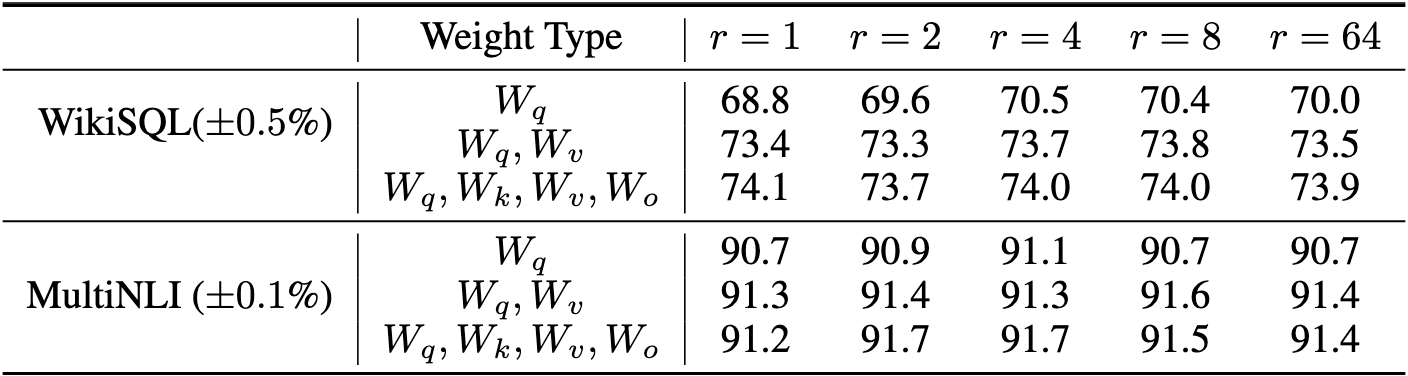
令我们惊讶的是，在这些数据集中，像一个这样的较小排名就足以适应 Wq 和 Wv，而单独训练 Wq 需要更大的 r。

增加 r 并不会覆盖更有意义的子空间，这表明低秩适应矩阵是足够的。

探讨不同秩的空间相似性

讨论在不同秩 $r$ 的情况下，LoRA 的低秩更新矩阵 $A_{r=8}$ 和 $A_{r=64}$ 的子空间相似性。通过子空间分析，解释了为何较低的 $r$（如 $r=1$ 或 $r=8$）能够在任务中表现良好。

研究目标

目标：
- 探索低秩分解中不同秩 $r$ 的矩阵 $A$ 是否共享重要的子空间。
- 进一步解释为何较低的秩（如 $r=1$ 或 $r=8$）仍能有效表示权重更新。
方法：
- 使用奇异值分解（SVD）得到适配矩阵 $A_{r=8}$ 和 $A_{r=64}$ 的右奇异向量矩阵（right-singular unitary matrices）： $U_{A_{r=8}}, U_{A_{r=64}}$
- 研究 $U_{A_{r=8}}$ 的前 $i$ 个奇异向量与 $U_{A_{r=64}}$ 的前 $j$ 个奇异向量之间的子空间重叠情况。

子空间相似性定义

子空间相似性度量：
- 使用基于 Grassmann 距离的归一化相似性指标来量化子空间重叠： $\phi (A_{r=8}, A_{r=64}, i, j) = \frac{\|\left (U_{A_{r=8}}^i\right)^T U_{A_{r=64}}^j\|_F^2}{\min (i, j)}$
  - $U_{A_{r=8}}^i$：$U_{A_{r=8}}$ 的前 $i$ 个奇异向量列。
  - $U_{A_{r=64}}^j$：$U_{A_{r=64}}$ 的前 $j$ 个奇异向量列。
  - $\phi$ 的值范围为 $[0, 1]$，其中：
    - $\phi = 1$：两个子空间完全重叠。
    - $\phi = 0$：两个子空间完全分离。
研究重点：
- 探索 $A_{r=8}$ 和 $A_{r=64}$ 在不同的 $i$ 和 $j$ 组合下的子空间重叠情况。
- 仅分析第 48 层的结果，但结果适用于所有层。

图表解析

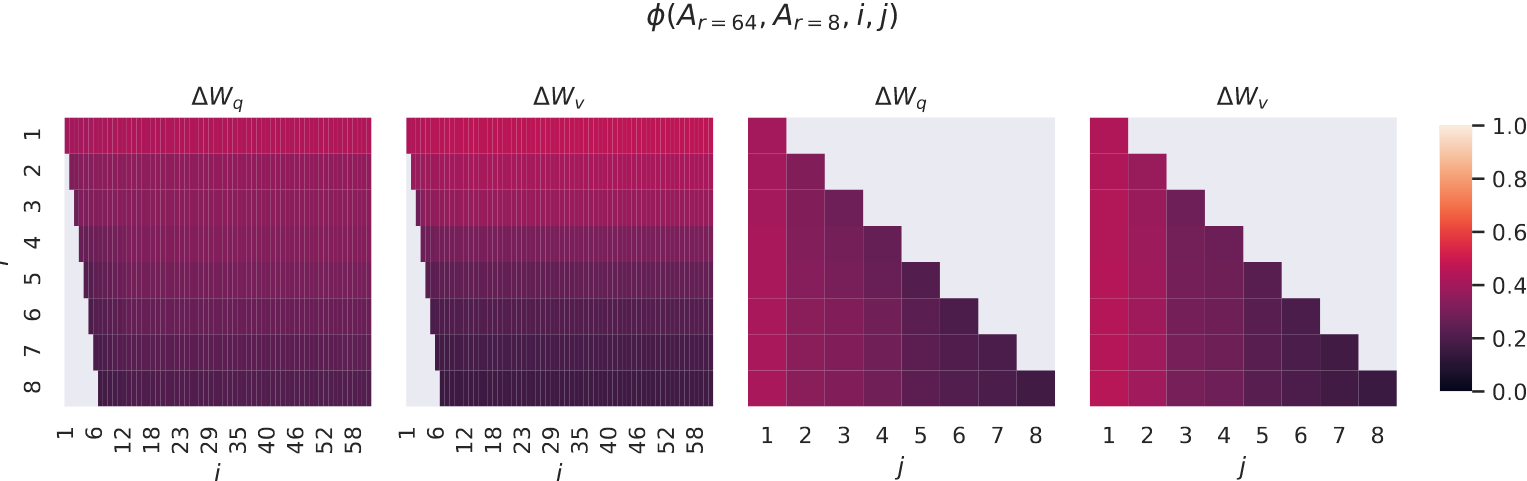
图 3 展示了子空间相似性 $\phi$ 的热图，分别针对权重更新矩阵 $\Delta W_q$ 和 $\Delta W_v$：

第一和第二图（左侧）：
- 代表 $A_{r=8}$ 和 $A_{r=64}$ 的子空间相似性，聚焦于 $i, j \leq 8$ 的情况。
- 左下角的部分放大，显示较低秩时的子空间重叠情况。
第三和第四图（右侧）：
- 代表相似性较高的方向（子空间重叠显著）。

关键观察

子空间重叠现象：
- $A_{r=8}$ 和 $A_{r=64}$ 的奇异向量子空间在前几个奇异向量方向上高度重叠（相似性 $\phi > 0.5$）。
- 说明低秩矩阵 $A_{r=8}$ 的重要方向已经包含在 $A_{r=64}$ 的子空间中。
噪声过滤作用：
- 更高秩的矩阵（如 $A_{r=64}$）包含更多奇异向量，但其中一些可能主要是噪声。
- 低秩矩阵（如 $A_{r=8}$）通过限制秩，有效过滤掉了这些噪声向量，从而提高了更新的有效性。
权重更新的重要方向：
- 对于 $\Delta W_v$ 和 $\Delta W_q$，前几个奇异向量的重叠性尤其显著，表明这些方向对任务适配最为重要。

结论与解释

子空间相似性说明了低秩的有效性：
- 尽管 $r=8$ 比 $r=64$ 的秩低得多，但它已经捕捉了任务适配所需的最重要方向。
- 因此，低秩的 LoRA 参数（如 $r=8$ 或更低）仍能在任务中表现良好。
解释低秩的表现：
- 低秩适配矩阵通过子空间共享，专注于最重要的方向，减少了对不必要方向（潜在噪声）的学习。
为什么 $r=1$ 仍然有效：
- 当 $r=1$ 时，虽然只有一个奇异向量，但这个方向与高秩矩阵（如 $r=64$）中的重要方向高度重叠，适配效果不会显著下降。

问题三：∆W 与 W 之间的关系

1. 研究问题

核心问题：
- $\Delta W$ 与 $W$ 的关系如何？
  - $\Delta W$ 是否与 $W$ 的重要奇异方向高度相关？
  - $\Delta W$ 是否主要放大了 $W$ 已有的重要方向，还是引入了新方向？
- 这些问题的答案可以揭示 LoRA 如何利用预训练模型权重进行下游任务的适配。

2. 分析方法

将 $W$ 投影到 $\Delta W$ 的子空间：
- 使用 $\Delta W$ 的左右奇异向量矩阵（通过 SVD 得到的 $U$ 和 $V$）定义子空间。
- 投影操作：计算 $U^T W V^T$，并与 Frobenius 范数 $|W|_F$ 比较，以量化 $W$ 的信息在 $\Delta W$ 子空间中的占比。
比较不同方向的相关性：
- 替换 $U$ 和 $V$ 为：
  - $\Delta W$ 的奇异向量（适配子空间）。
  - $W$ 的前 $r$ 个奇异向量（预训练模型的重要方向）。
  - 随机高斯矩阵的奇异向量（随机方向）。
- 比较投影结果的 Frobenius 范数，分析 $\Delta W$ 的相关性。

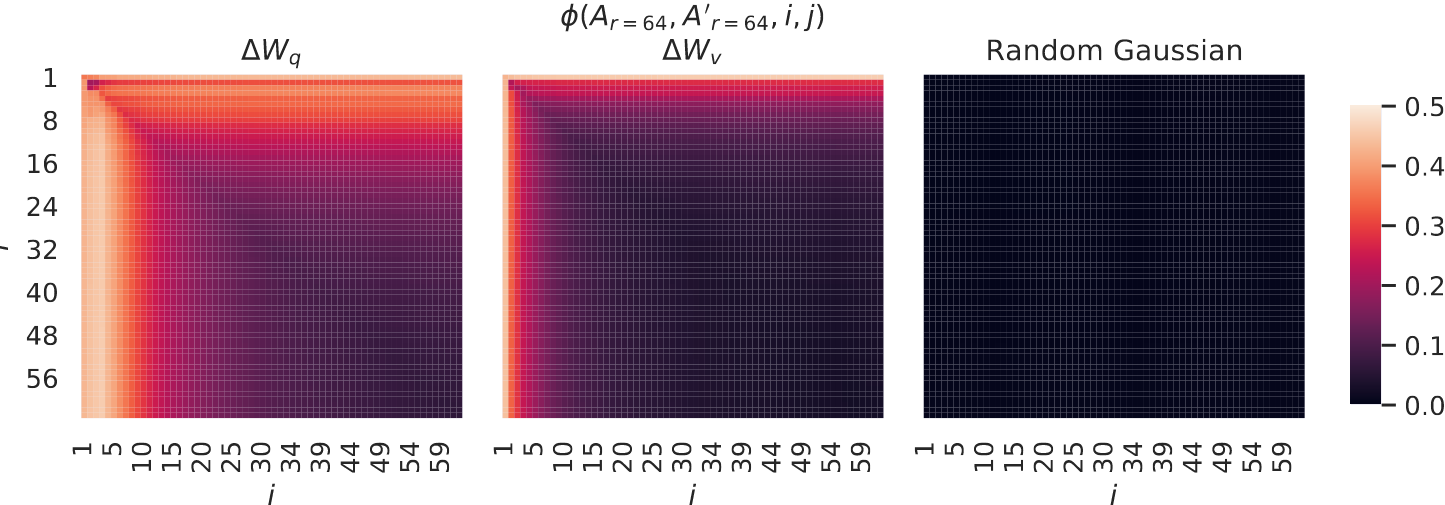
3. 图 4 的热图分析

左图和中图（$\Delta W_q$ 和 $\Delta W_v$）：
- 显示了两个随机种子下，$\Delta W_q$ 和 $\Delta W_v$ 的列向量相似性。
- 可以看到，相似性较高的方向集中在前几个奇异向量，说明适配的矩阵捕获了主要的变化方向。
右图（随机高斯矩阵的相似性）：
- 显示了随机矩阵的奇异向量相似性，几乎没有任何结构（接近 0），表明 $\Delta W$ 的方向与随机噪声完全不同。

4. 表格 7 的数据分析

表格展示了不同投影方向下的 Frobenius 范数对比：

$|U^T W_q V^T|_F$：
- 这是将 $W_q$ 投影到不同子空间后的范数：
  - 对比 $\Delta W_q$、$W_q$ 自身、随机矩阵的子空间。
- $r=4$：
  - 投影到 $\Delta W_q$ 的子空间后，范数为 $0.32$，远小于投影到 $W_q$ 的 $21.67$，表明 $\Delta W_q$ 并没有简单重复 $W_q$ 的奇异方向。
  - 投影到随机矩阵的范数为 $0.02$，进一步验证 $\Delta W_q$ 的方向并非随机。
- $r=64$：
  - 投影到 $\Delta W_q$ 的子空间后，范数为 $1.90$，仍然小于 $W_q$ 的 $37.71$。
$|\Delta W_q|_F$：
- 适配矩阵 $\Delta W_q$ 的范数为 $6.91$（$r=4$）和 $3.57$（$r=64$）。
- 说明随着 $r$ 增加，适配矩阵的强度逐渐降低。

5. 关键结论

$\Delta W$ 不是简单重复 $W$：
- 投影结果表明，$\Delta W$ 的子空间与 $W$ 的重要方向部分重叠，但也包含了额外的新方向。
- 适配矩阵的作用是放大 $W$ 中已有的部分方向，同时引入对任务有用的新方向。
适配矩阵的放大因子较高：
- 表格中提到，对于 $r=4$，$\Delta W_q$ 的放大因子高达 $21.5 = 6.91 / 0.32$，表明 LoRA 更倾向于放大重要特征，而不是重复预训练模型已有的权重分布。
低秩适配有效性：
- 尽管 $r$ 较低（如 $r=4$），$\Delta W$ 的低秩方向仍能捕获适配的核心特征，并显著增强下游任务的表现。

上篇DPO论文学习

下篇Tool Learning with Foundation Models 论文笔记