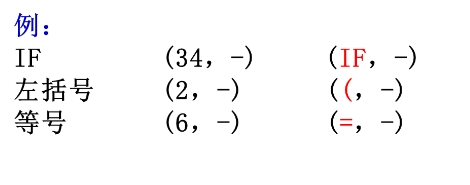编译原理笔记

[TOC]

第一章绪论

什么是编译程序

把某一种高级语言程序等价的转换成另一种低级语言程序的程序

编译器的各个阶段

源程序 词法分析 语法分析 语义分析与中间代码产生 代码优化 代码生成

第二章高级语言及其语法描述

语法

一组规则，用它可以形成和产生一个合适的程序

词法规则：单词符号的形成规则

1. 语法规则和词法规则定义了程序的形式结构
2. 定义语法单位的意义属于语义问题

语义

一组规则，用它可以定义一个程序的意义

描述方法：属性文法

程序语言的语法描述

一些概念

• 有穷字母表$\sum$ : 又叫字符集，其中每一个元素称为一个字符
• 例子：$\sum$ = {a-z, A-Z,0-9}
• $\sum$上的字（字符串）是指由$\sum$ 中的字符所构成的有穷序列
• 不含任何字符的称为空字 记为 $\epsilon$

• $\sum ^ *$ 表示 $\sum$ 上的左右字的全，包含空字

• 连接（积）

  

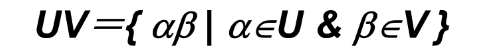
• n次积 $V^n=VV\dots V$

• 闭包：

• 正则闭包：$V^+ = V V^*$

上下文无关文法

文法：描述语言的语法结构的形式规则（或语法规则）

上下文无关文法 ：是一个四元式 G=($V_T,V_N,S,P$)

• VT：终结符集合（非空）V，就是句子中的单词

• VN：非终结符集合（非空），且V， V=0

• S：文法的开始符号，SEYN 必须属于某个产生式的左部

• P：产生式集合（有限），每个产生式形式为

  P→a, PeVN a E (VyUVN)* P就是规则

然后由此我们可以完善一下相关概念

• 直接推出：
• 推导：如果$\alpha \rightarrow \alpha_2 \dots \rightarrow \alpha_n$，则我们称这个序列是从c，到a，的一个推导。若存在一个从a到an的推导，则称a可以推导出an。
• 一步或若干步推导：通常，用$\alpha_1 \rightarrow^+ a_n$，表示：从a出发，经过一步或若千步，苛以推出an。
• 0步或若干步推导：通常，用$\alpha_1 \rightarrow^* a_n$，表示：从a出发，经过一步或若千步，苛以推出an
• 句型：定义：假定G是一个文法，S 是它的开始符号。如果$S\rightarrow^* \alpha$则a称是一个句型。
• 句子：仅含终结符号的句型是一个句子。
• 语言：文法G所产生的句子的全体是一个语言，将它记为 L（G）。

应用（做题）

文法-》语言

语言-》文法

语法树与二义性

文法二义性：果一个文法存在某个句子对应两棵不同的语法树，则说这个文法是二义的。

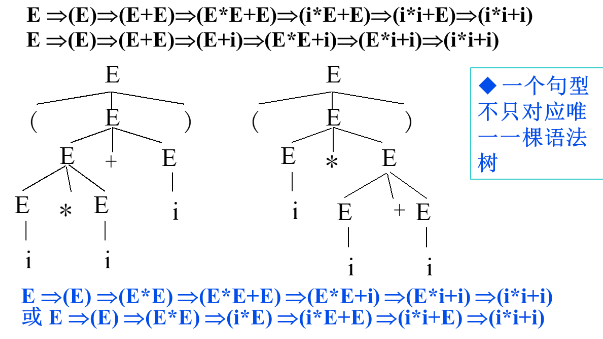
语言二义性：一个语言是二义的，如果对它不存在无二义的文法。语言不是二义性就是，存在一个文法不是二义性的。

第三章词法分析

词法分析器

功能和输出形式

功能：输入源程序、输出单词符号

单词符号的种类

• 基本字：如begin，repeat，……
• 标识符：表示各种名字，如变量名，数组名和过程名
• 常数：各种类型的常熟
• 运算符：+，-，* ，/ ,……
• 界符：逗号，分号、括号和空白

输出的单词符号的表示形式：（单词种别，单词自身的值）

单词种别通常用整数编码表示

• 若一个种别只有一个单词符号，则种别编码就代表该单词符号。假定基本字、运算符和界符都是一符一种。
• 若一个种别有多个单词符号，则对于每个单词符号，给出种别编码和自身的值。 •标识符单列一种；标识符自身的值表示成按机器字节划分的内部码。 •常数按类型分种；常数的值则表示成标准的二进制形式。

例子:

助忆符：直接用编码表示不便于记忆，因此用助忆符表示编码

例子

作为一个独立子程序

词法分析是作为一个独立的阶段，是否应当将其处理为独立的一遍呢？

• 作为独立阶段的优点： 使整个编译程序结构简洁、清晰和条理化， 有利于集中考虑词法分析一些枝节问题。
• 不作为独立的一遍： 将其处理为一个子程序。

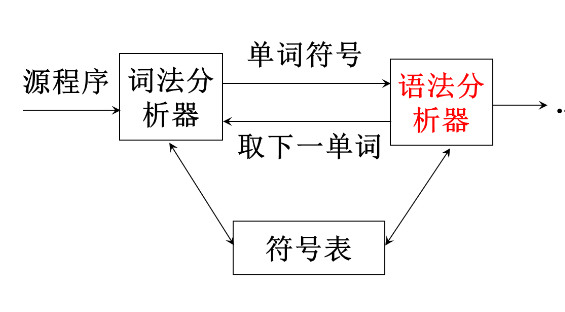
词法分析器的设计

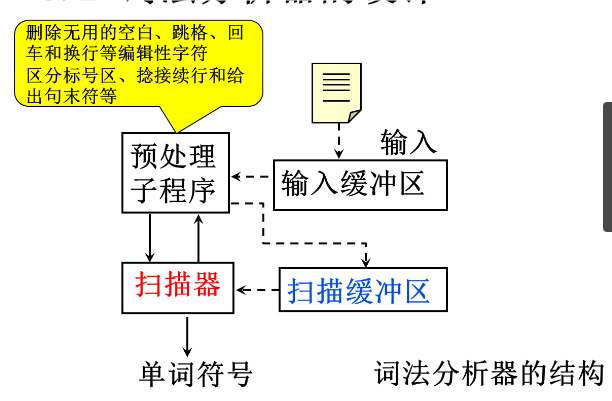
扫描缓冲区的设计

超前搜索

• Fortran语言基本字的识别： • Fortran语言书写时可不写空格，看起来方便，却给编译程序带来很大的困难！Fortran语言的基本字不叫保留字，因为它的关键字可以作为普通的标识符用。例如： （1） DO99K是什么意思？

DO99K=1,10 DO 99 K= 1,10 //99是标号
DO99K=1.10
// DO99K是标识符

（2） IF是基本字，还是普通标识符？

IF (5. EQ.M) GOT055 IF (5. EQ.M) GOTO 55
IE （5）=55
// IF是数组名

• 需要超前搜索才能确定哪些是基本字

需要超前搜索的情况

• 标识符识别 字母开头的字母数字串，后跟界符或算符
• 常数识别
  • 识别出算术常数并将其转变为二进制内码表 示。有些也要超前搜索。 5.EQ.M
• 算符和界符的识别
  • 把多个字符符合而成的算符和界符拼合成一个单一单词符号。 ；，**，，EQ.十，：>=

不必使用超前搜索的条件

• 所有基本字都是保留字；用户不能用它们作自己的标识符； 基本字作为特殊的标识符来处理；不用特殊的状态图来识别，只要查保留字表。
• 如果基本字、标识符和常数（或标号）之间没有确定的运算符或界符作间隔，则必须使用一个空白符作间隔

词法分析器的设计流程

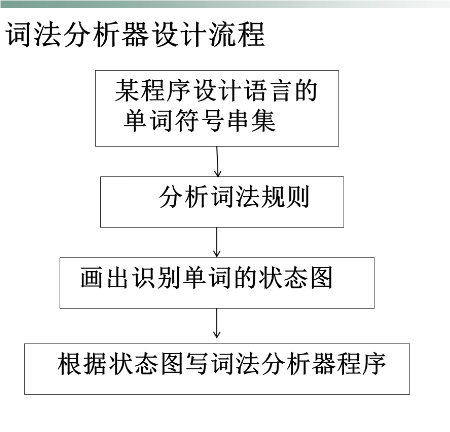
正规表达式与有限自动机

• 字符集：考虑一个有穷字母表∑ 字符集

• 字符：其中每一个元素称为一个字符

• 字符：∑上的字(也叫字符串) 是指由∑中的字符所构成的一个有穷序列

• 空字：不包含任何字符的序列称为空字，记为 ε

• 全体：用∑*表示∑上的所有字的全体,包含空字ε

  例如:设={a，b}，则 ∑*={ε,a b,aa,ab,ba,bb,aaa,…}

• 连接（积）：∑*的子集U和V的连接(积)定义为

  UV={aβ| αeU & BeV} V自身的 n次积记为 Vn=VV…V

• 正规闭包：规定Vo={ε}，令 V=VoUV1UV2UV3U… 称V“是V的闭包: 记 V+≡V∨，称V*是V的正规闭包

正规式和正规集的关系

正规集可以用正规表达式(简称正规式)表示。 正规表达式是表示正规集一种方法。 一个字集合是正规集当且仅当它能用正规式表示。

正规式

对给定的字母表$\sum$

1. ε和∅都是上的正规式，它们所表示的正规集为 {ε} 和Ø;

2. 任何$a \in \sum$​，a是Z上的正规式，它所表示的正规集为{a};

3. 假定e和e,都是Σ上的正规式，它们所表示的正规集为L(e,)和L(ez)，则
   1. (e l ez)为正规式，它所表示的正规集为L(ej)uL(ez);
   2. (e.ez)为正规式，它所表示的正规集为L(e,)L(ez)(连接积)
   3. (e)*为正规式，它所表示的正规集为 (L(e,))(闭包，即任意有限次的自重复连接)

仅由有限次使用上述三步骤而定义的表达式才是Z上的正规式，仅由这些正规式表示的字集才是∑上的正规集。

• 所有词法结构一般都可以用正规式描述
• 若两个正规式所表示的正规集相同，则称 这两个正规式等价。如 b(ab)*=(ba)*b (a*b*)*=(alb)

确定有限自动机（DFA）

确定有限自动机M是一个五元式M=（S, 2, f, So,F），其中

1. S：有穷状态集，
2. 2：输入字母表（有穷），
3. f：状态转换函数，为SxZ-S的单值映射函数 f（S,a）=s’表示：当现行状态为S，输入字符为 a时，将状态转换到下一状态s’。我们把s’ 称为s的一个后继状态。
4. $S_0$是唯一的一个初态；
5. FS：终态集（可空）。

非确定有限自动机（NFA）

非确定有限自动机（NFA）M是一个五元式M=（S, 2, f, So,F），其中

1. S：有穷状态集，
2. $\sum$：输入字母表（有穷），
3. f：状态转换函数，为$S_x\sum^* \rightarrow 2^S$的部分映射(非单值）
4. $S_0 \in S$是非空的初态集
5. F：终态集（可空）。

NFA M 所示别的字符串的全体记为L（M）

NFA和DFA的区别

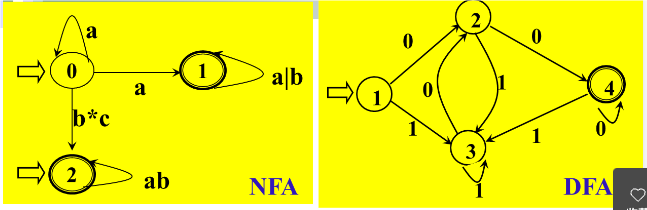
从状态图可看出NFA 和DFA的区别：

1. NFA可有多个初态
2. NFA弧上的标记可以是$\sum^*$中的一个字（甚至可以是一个正规式），而不一定是单个字符；
3. NFA同一个字可能出现在同状态射出的多条弧上。

所以 DFA是NFA的特例。

NFA与DFA的转换

理论基础

自动机等价定义：对于任何两个有限自动机M和M’，如果L（M）=L（M’），则称M与M’等价。

自动机理论中一个重要的结论：判定两个自动机等价性的算法是存在的。

对于每个NFA M存在一个DFA M’，使得L（M）=L（M’）。亦即DFA与NFA描述能力相同。

NFA转换为等价的DFA

假定NFA M=<S,2, 6,So, F>，我们对NFA M的状态转换图进行以下改造：

1. 引进新的初态结点X和终态结点Y，X,Y¢S， 从X到S。中任意状态结点连一条$\epsilon$箭弧，从F中任意状态结点连一条e箭弧到Y。

2. 按以下3条规则对NFA M的状态转换图进一步施行替换，直到把这个图转变为每条弧只标记 $\sum$上的一个字符或$\epsilon$；其中k是新引入的状态。

   

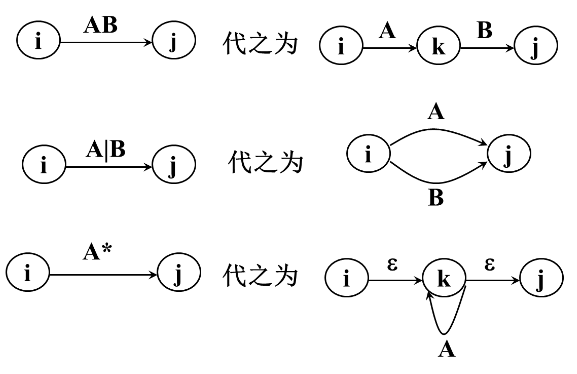
   例子

   

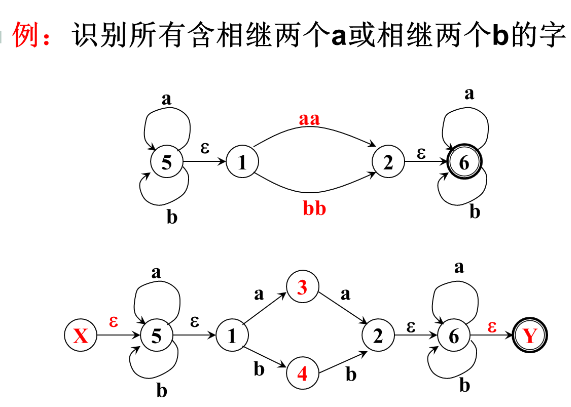
3. 将上述NFA确定化——采用子集法

   理论：

   闭包定理

   设I是NFA的状态集的一个子集，定义I的$\epsilon$-闭包：$\epsilon$-closure（I）为：

   1. 若$s \in I$，则$s \in \epsilon$-closure（I）；
   2. 若$s \in I$，则从s出发经过任意条$\epsilon$弧而能到达的任何状态s’都属于$\epsilon$-closure（I） 即e-closure（I）={s’ | 从某个$s \in I$出发经过任意条：弧能到达s’｝

   $I_a$定义

   设a是2中的一个字符，定义 \(I_a=\epsilon-closure(J)\) 其中，J为I中的某个状态出发经过一条a弧而到达的状态集合。

   

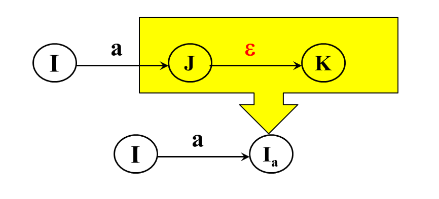
   例子

   

   

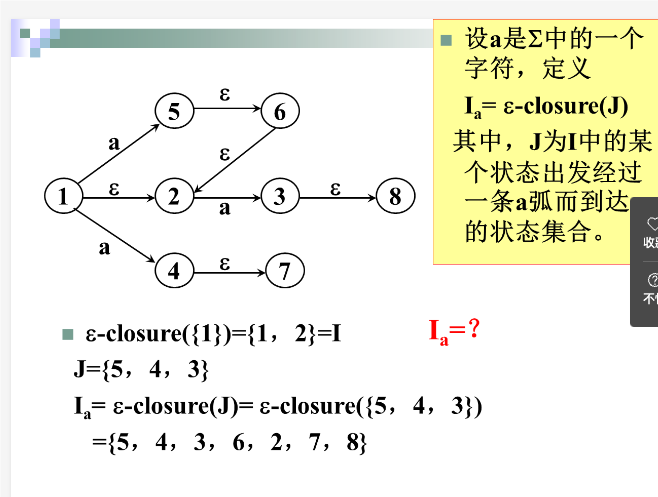
   例子

   

   

   

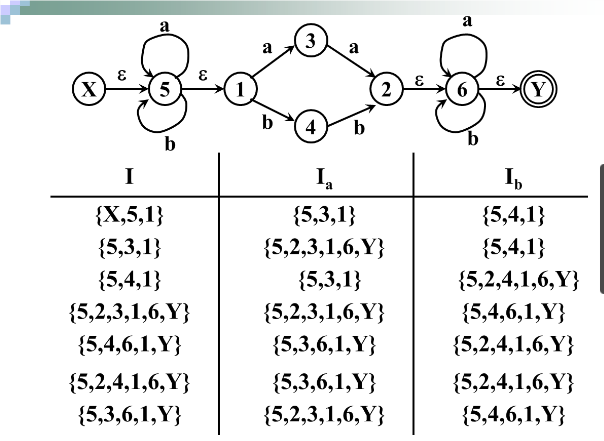
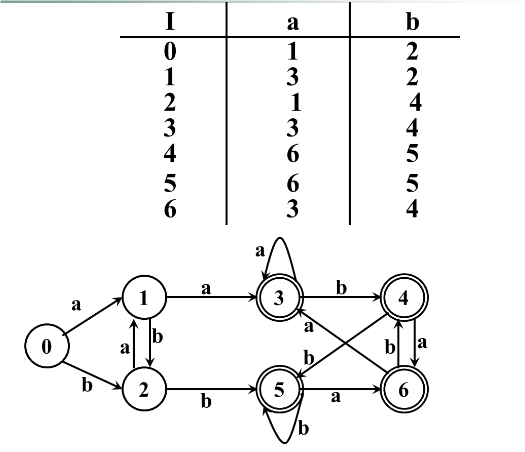
有限自动机转换为正规式

理论：

NFA->R(正规式)

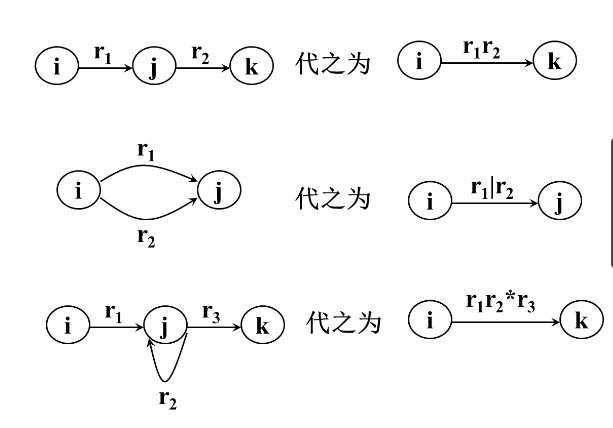
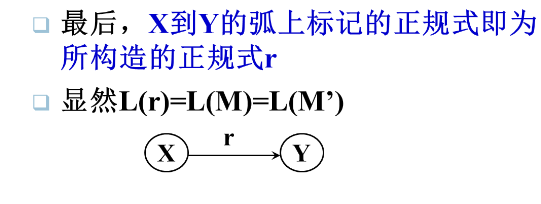
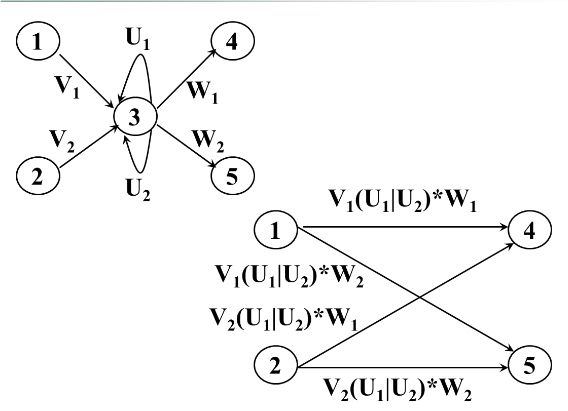
例子：

r->NFA

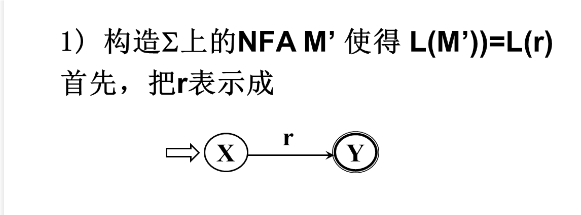
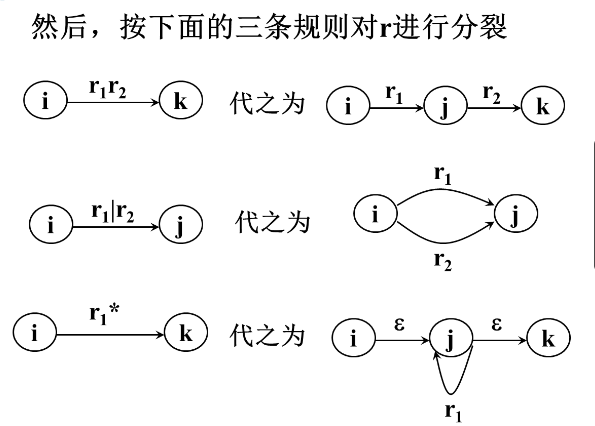
例子：

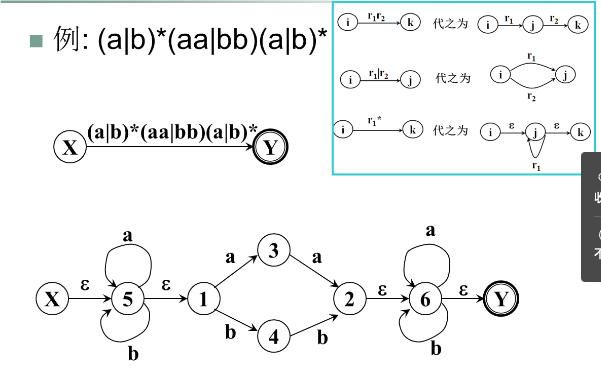
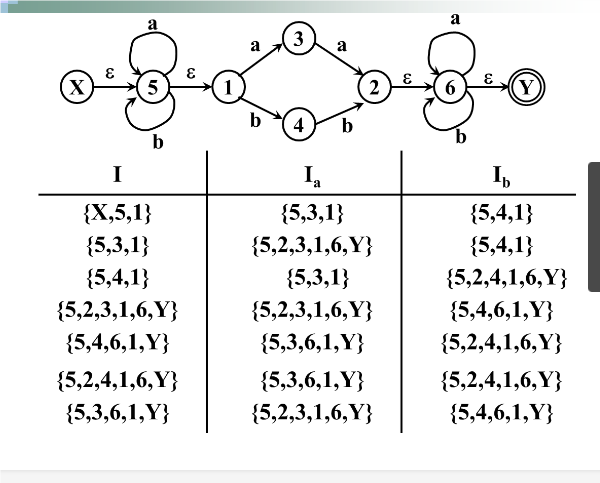
DFA（确定有限自动机）化简(DFA最小化)

目的（我们要干什么）

基本思想：

怎么做

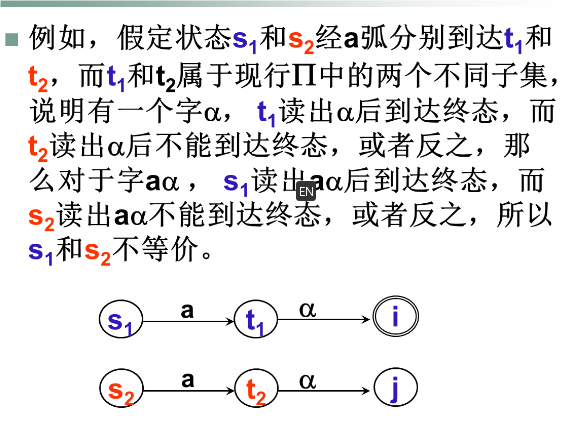
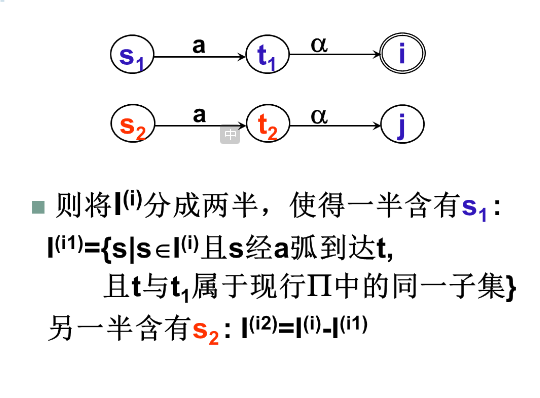
注意要分成N个分组

例子：

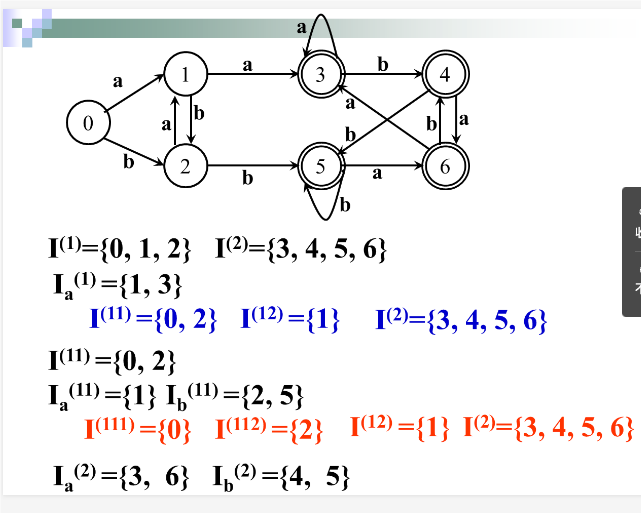
第四章语法分析 自上而下分析

语法分析

使用上下文无关文法对语言的语法结构进行描述

语法分析的任务是分析一个文法的句子结构

语法分析器的功能：按照文法的产生式（语言的语法规则），识别输入符号串是否为一个句子

这里就要判断，看能否从文法的开始符号出发推导出这个输入串，或建立一棵与输入串匹配的语法树

语法分析的方法：

1. 自下而上

   1. 从输入串开始，逐步进行归约，直到文法的开始符号
   2. 归约根据文法的产生式规则，把串中出现的产生式的右部替换成左部符号
   3. 从树叶节点开始，构造语法树
   4. 算符优先分析法，LR分析法

2. 自上而下

   1. 从文法的开始符号出发反复使用各种产生式，寻找『匹配』的推导
   2. 推导：根据文法的产生式规则，把串中出现的产生式的左部符号替换成右部
   3. 从树的根开始，构造语法树
   4. 递归下降分析法、预测分析程序

LL(1)分析法

消除左递归

例子

消除回溯

提取公共左因子

如果一个非终结符的候选FIRST相交则使用提取公共左因子，来使得两两不相交

判断是否是LL(1)文法

(3)的原因

FIRST 集合与 FOLLOW 集合：

• FIRST(A)：表示从非终结符 A 推导出的字符串的首字符的集合。
• FOLLOW(A)：表示所有在文法中能够出现在 A 之后的符号集合。

条件(3) 的要求：

• 如果存在某个候选首符集合包含 ε（空串），则要求 FIRST(A) 与 FOLLOW(A) 的交集为空集合，即 FIRST(A) ∩ FOLLOW(A) = ∅。

原因：

• 如果非终结符 A 的某个候选首符集合包含 ε，意味着 A 可以推导出空串。
• 这种情况下，如果 FOLLOW(A) 中的某个符号也在 FIRST(A) 中存在，则当解析器遇到这个符号时，就无法确定是因为 A 推导出了空串还是需要使用 A 的其他产生式进行推导，导致解析器产生歧义。
• 通过要求 FIRST(A) ∩ FOLLOW(A) = ∅，可以避免这种歧义，从而使文法成为 LL(1) 文法，保证解析器可以顺利进行自上而下的分析而不会回溯。

求解FIRST集

定义：

$FIRST(\alpha)$指从$\alpha$所能推导出的所有串的首终结符结合

求法：

求解FOLLOW集

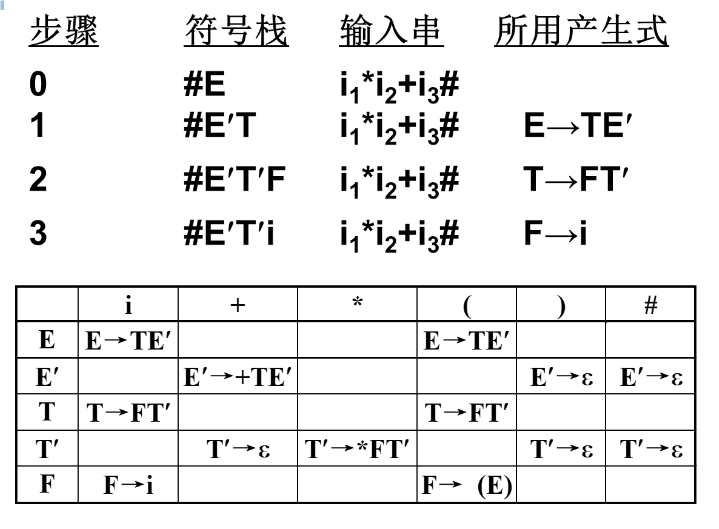
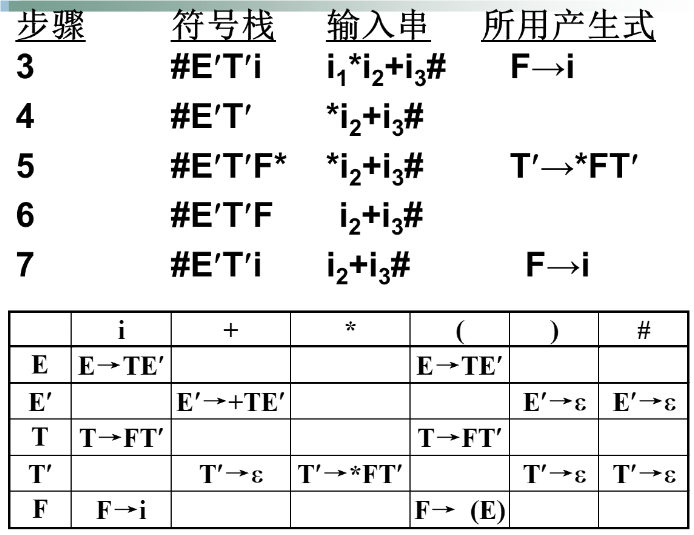
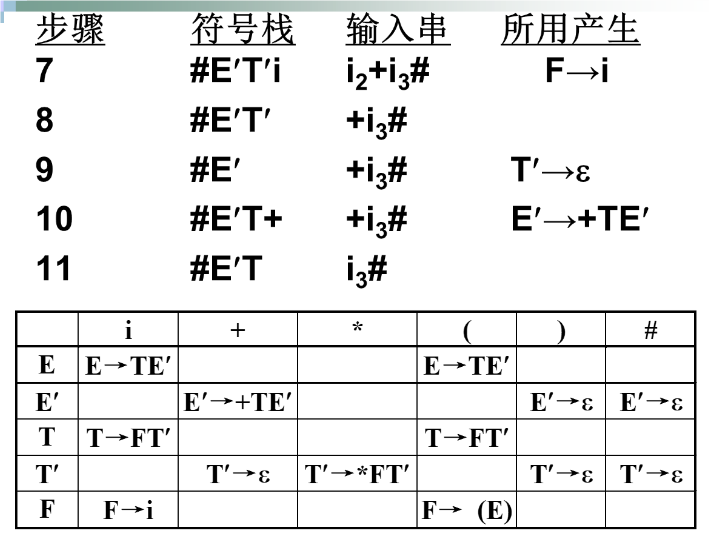
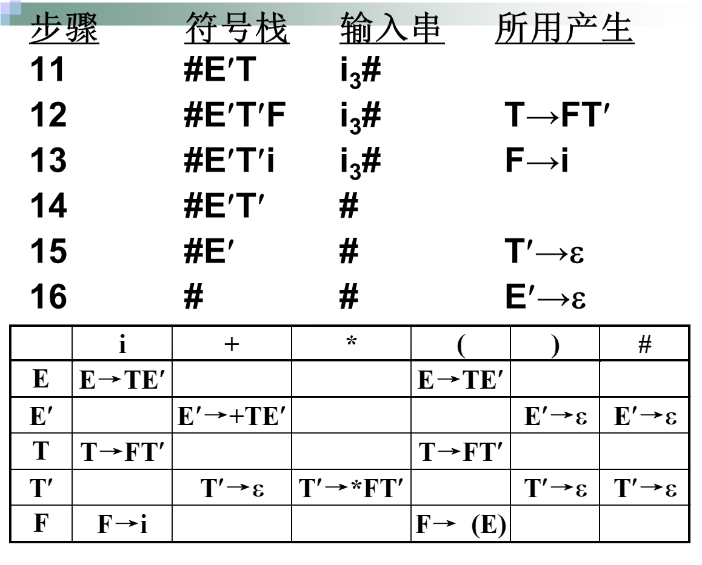
预测分析程序

根据当前输入符号，为当前要处理的非终结符选择产生式

利用预测分析表进行分析(总控程序)

例子：

预测分析表的构造

第五章 语法分析——自下而上分析

基本思想：用一个寄存符号的先进后出栈，把输入符号一个一个地移进到栈里，当栈顶形成某个产生式的候选式时，即把栈顶的这一部分替换（归约为）该产生式的左部符号

核心问题：识别可归约串

一些概念

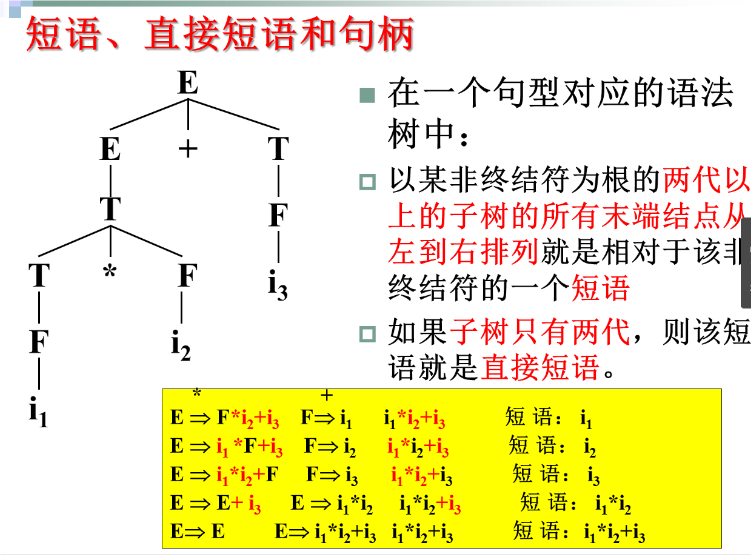
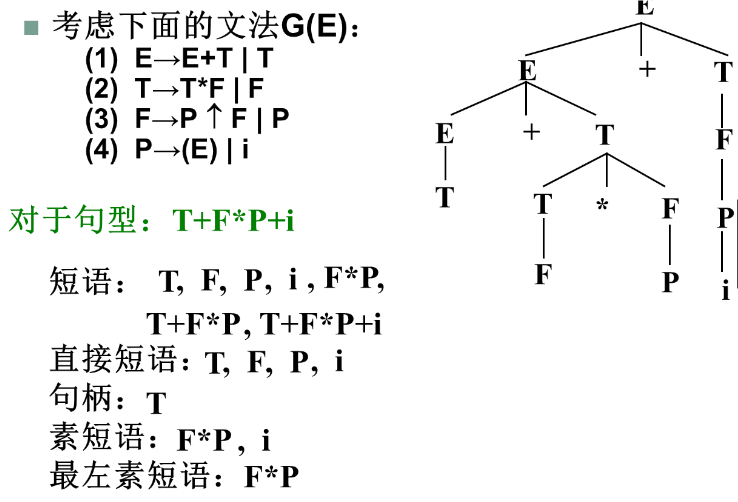
短语：

例子

规范规约

符号栈

算符优先分析

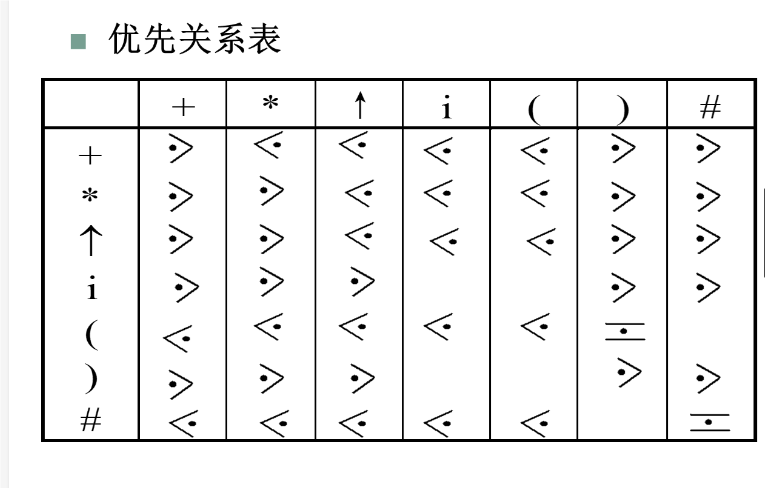
优先关系定义

算符文法定义

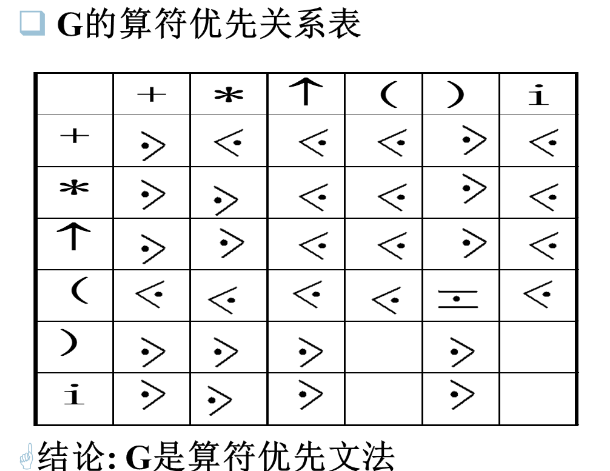
判断优先关系+判断算符优先文法

文法中任何两个终结符之间的关系必须满足下列三种关系之一，才是算符优先文法

例子

构造优先关系表算法

求FIRSTVT

求LASTVT(P)

构造优先关系表

例子

最左素短语

例子

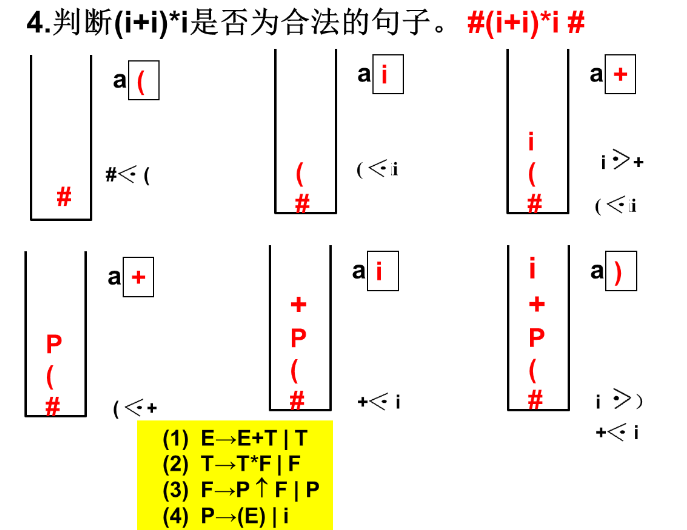
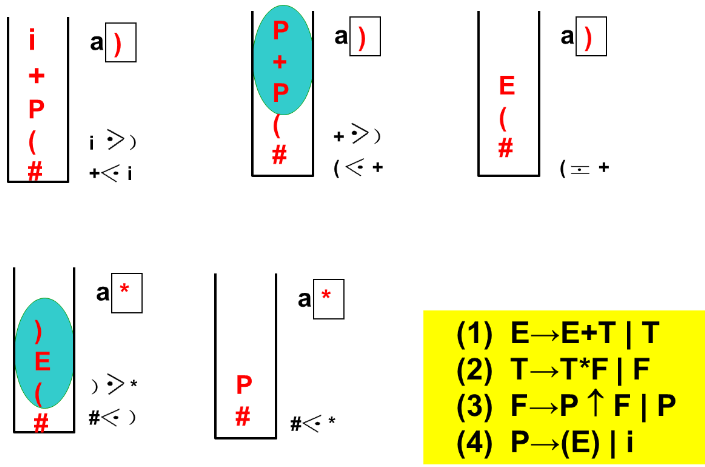
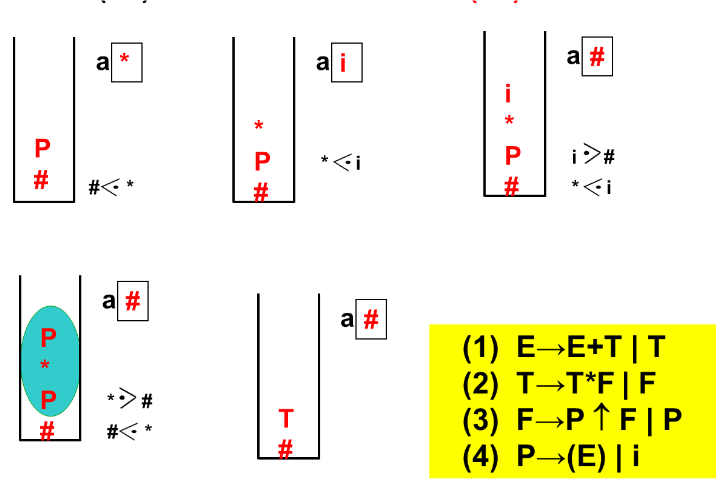
算符优先分析过程

例子

LR（0） 分析

一些概念

活前缀

项目

#例子

拓广文法

加入S’

然后拆成单个文法

步骤一 构造项目集规范族

两种情况：

情况1后面是终结符：

情况2：后面是非终结符（要把左边是该非终结符的产生式全部搬过来

####例子

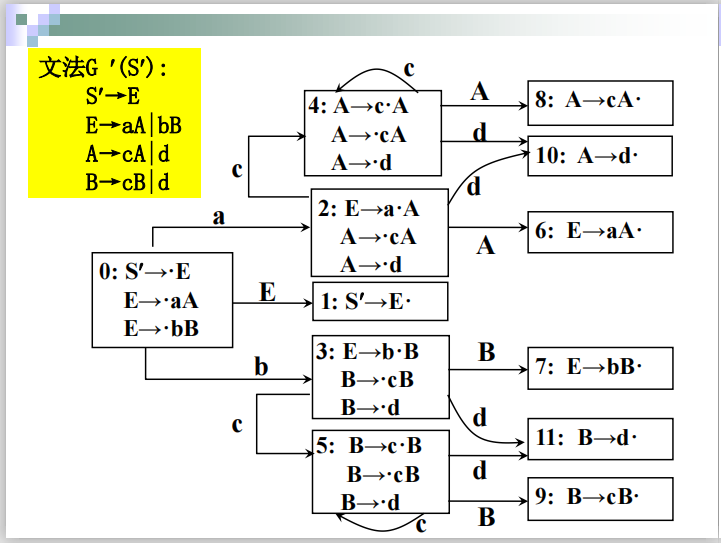
步骤二构造LR（0）分析表

算法

####例子

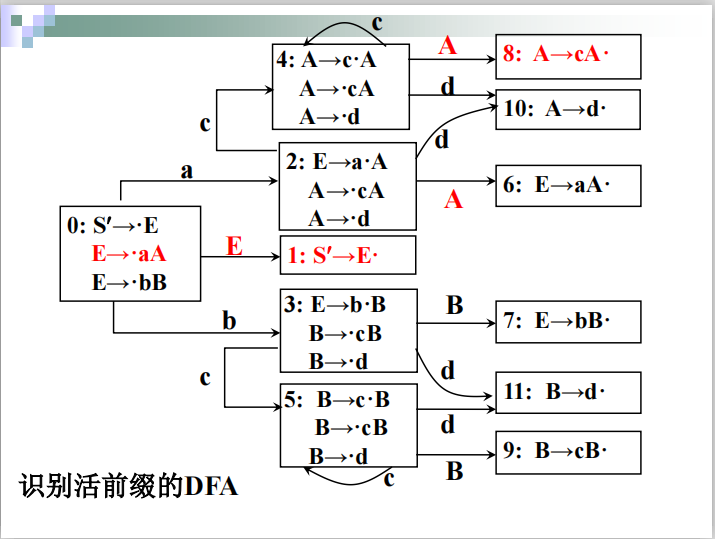
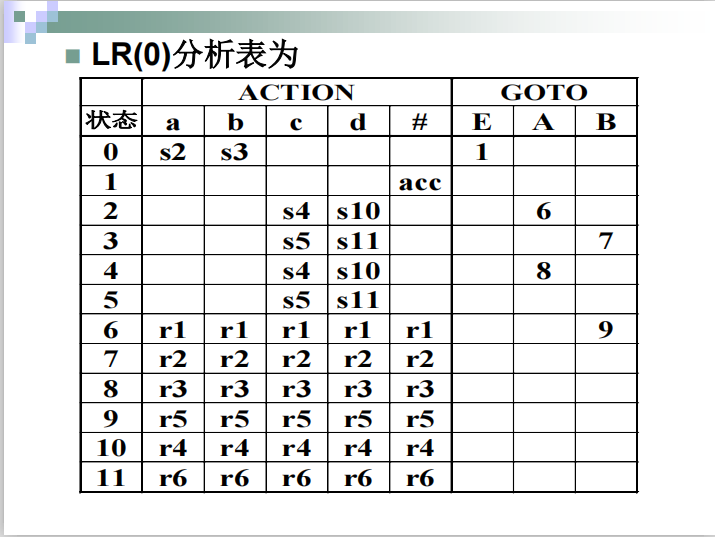
步骤三 使用LR（0）分析表

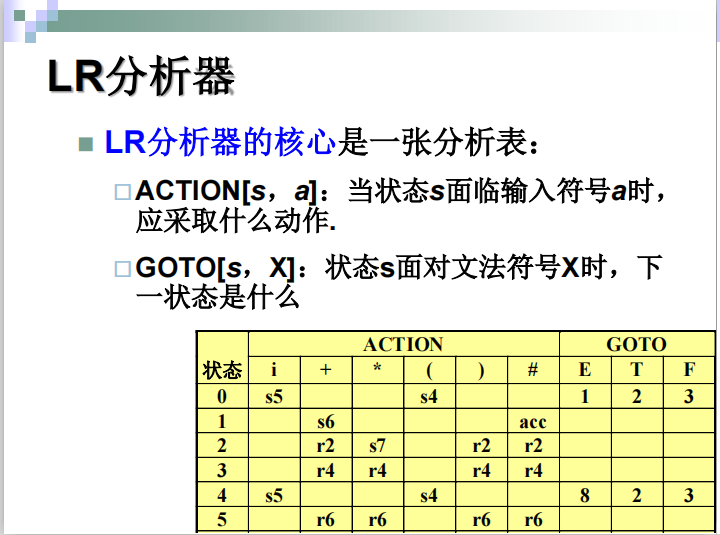
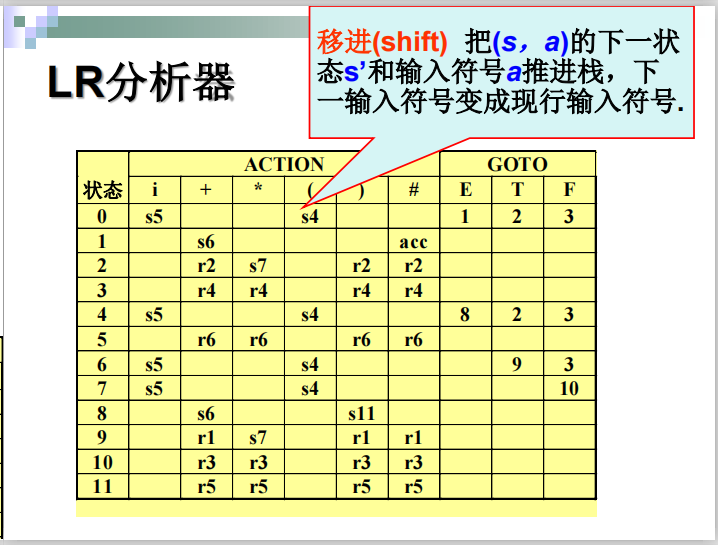
归约详细解释：

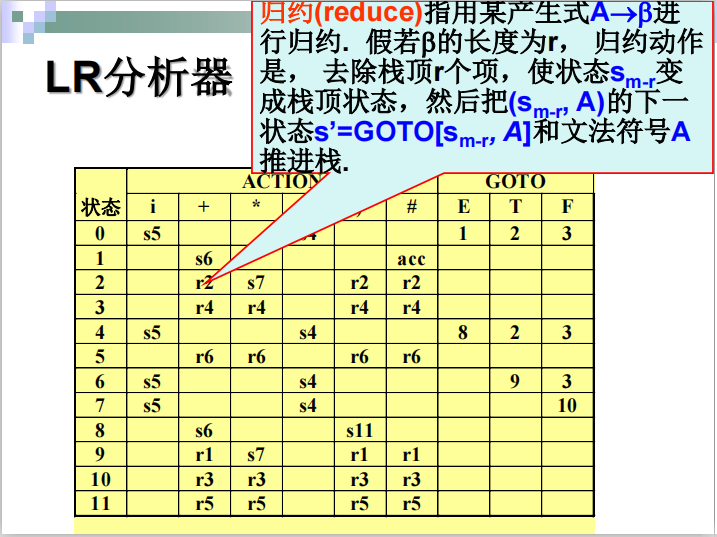（此图可能归约讲不清楚，建议看详细解释）

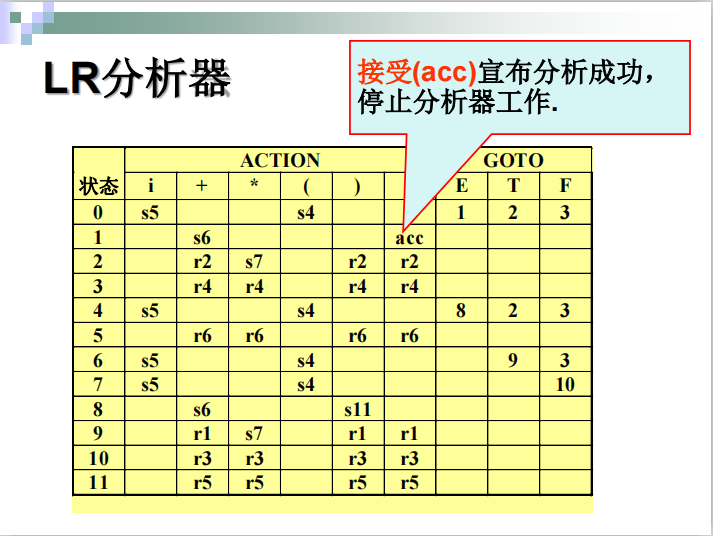
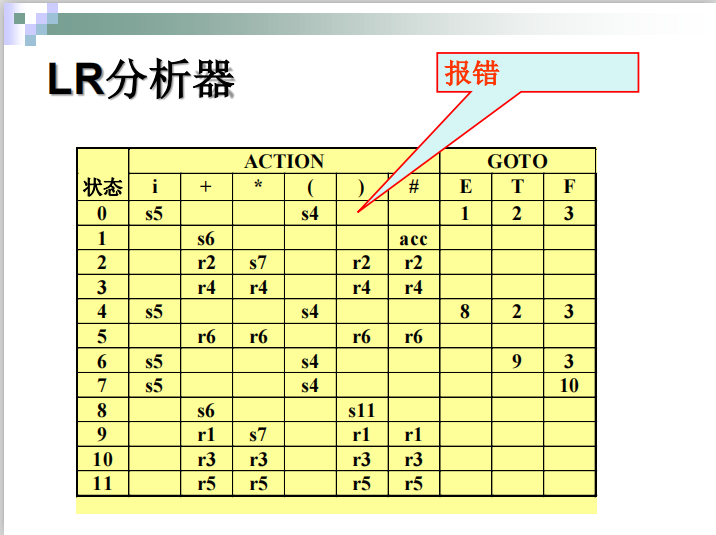
####例子

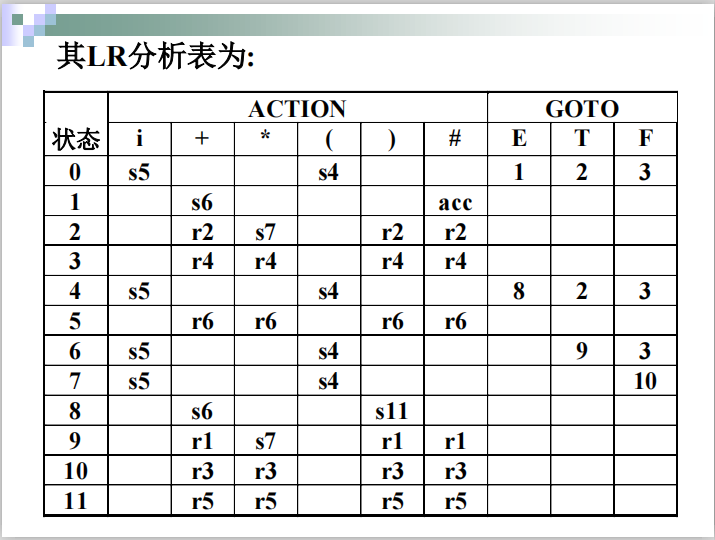
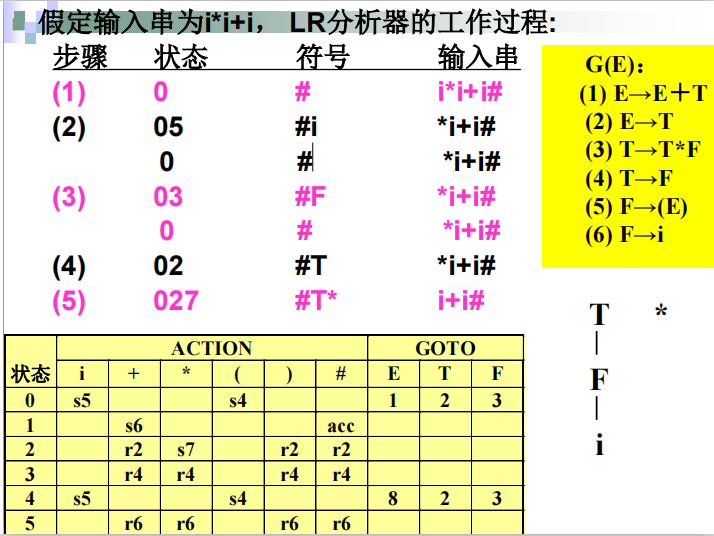
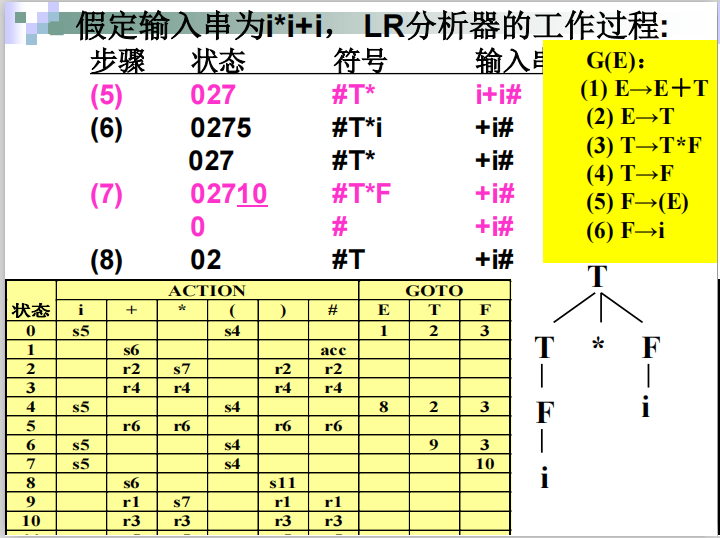
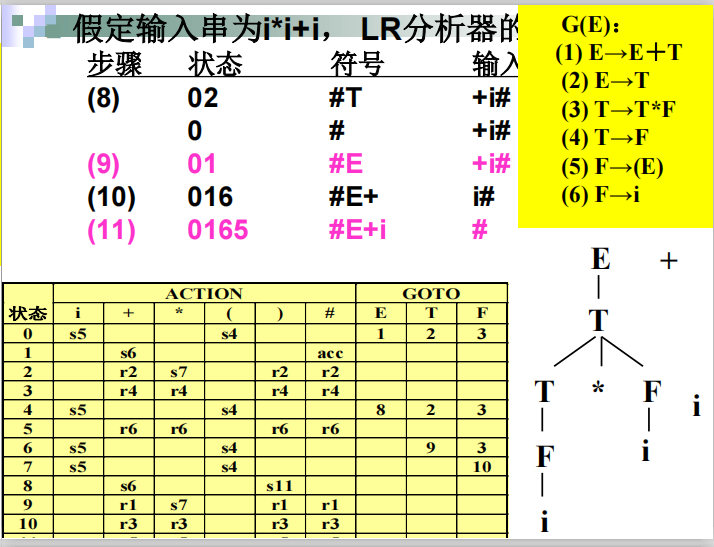
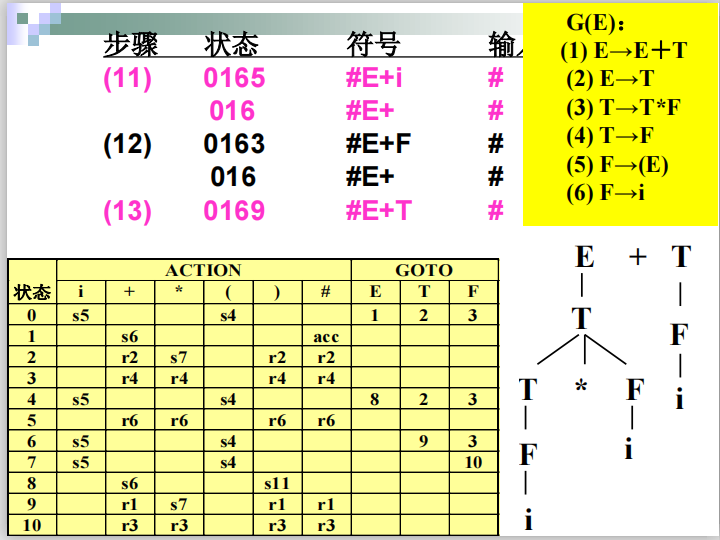
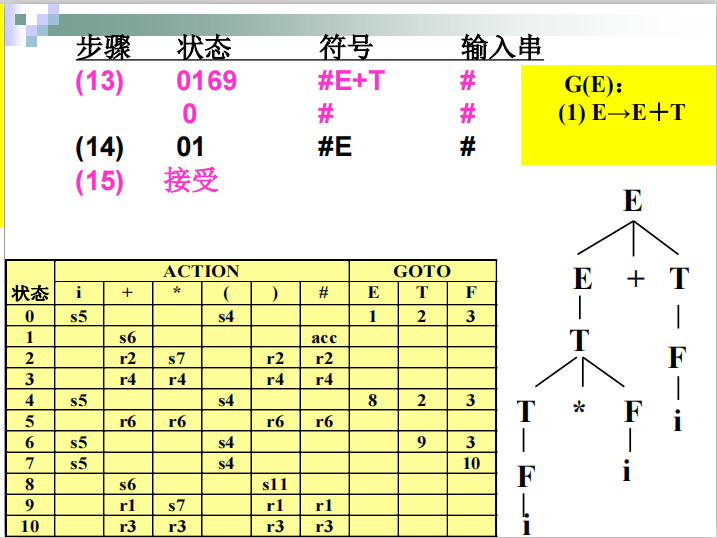
SLR（1）分析

判断LR(0)是否是SLR（1）文法

判断移进—归约冲突是否可解决

判断FOLLOW(S’)和{+}是不是有交集

判断FOLLOW(E)和{*}是不是有交集

归约的左边和移进的终结符

判断归约归约冲突是否可解决

如果是规约规约冲突 就把两个左边的FOLLWO集相交

解决冲突（SLR（1）与LR（0）的区别）

构造SLR（1）分析表算法

LR（1）分析

判断是否是LR（1）文法

先构造向前搜索符的的文法

然后再判断是否有移进归约冲突、归约归约冲突并且是否可消解，只不过是把follow集换成向前搜索符号

例子：

构造LR（1）项目集规范族

构造LR（1）分析表

LALR(1)

就是在LR（1）的基础上，增加合并同心集，相同产生式不同向前搜索符。

判断是否是LALR（1）与LR（1）相同

第六章属性文法和语法制导翻译

属性文法

S—属性文法

仅仅使用综合属性的文法成为S—属性文法。

例子：

L-属性文法

仅仅使用继承属性的文法称为L—属性文法

基于属性文法的处理方法

基于属性文法的处理过程通常为：

输入串——》语法树——》按照语义规则计算属性

• 这种由源程序的语法结构所驱动的处理方法就是语法制导翻译法
• 语义规则的计算
  • 产生代码
  • 符号表中存放信息
  • 给出错误信息
  • 执行任何其他动作
• 对输入符号串的翻译也就是根据语义规则进行计算的结果

一遍扫描的处理方法

一遍扫描的处理方法是在语法分析的同时计算属性值

• L—属性文法适合于一遍扫描的自上而下的分析
• S—属性文法适合于一遍扫描的自下而上分析

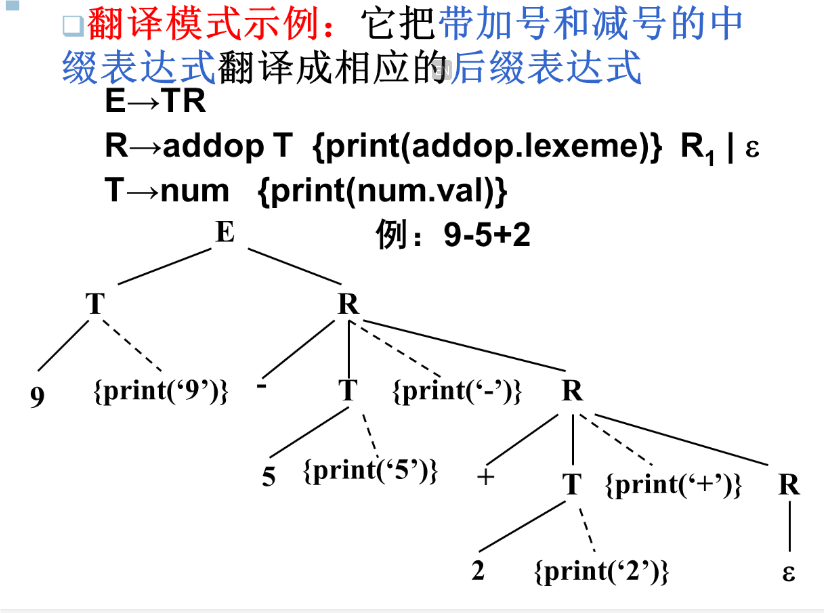
翻译模式

语法规则：给出了属性计算的定义，没有属性计算的次序等实现细节

翻译模式：给出了使用语义规则进行计算的次序，这样就可以把某些实现细节表示出来。

在翻译模式中，和文法符号相关的属性和一样规则（这里我们称语义动作），用花括号括起来插入到产生式右部的合适位置上

例子：

第七章语义分析和中间代码产生

中间语言

• 常用的中间语言：

  • 后缀式，又叫逆波兰表示

  • 图表示：DAG图、抽象语法树

  • 三地址代码

    • 三元式
    • 四元式
    • 间接三元式

后缀式

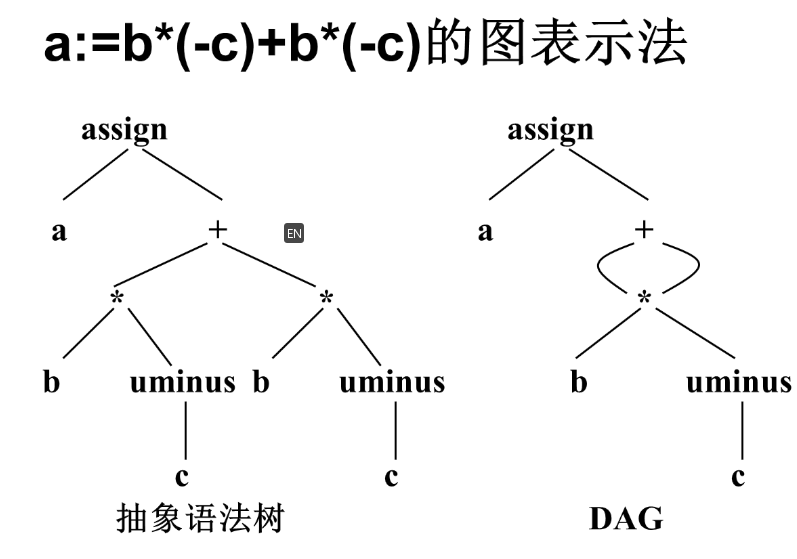
图表示法

• DAG
• 抽象语法树

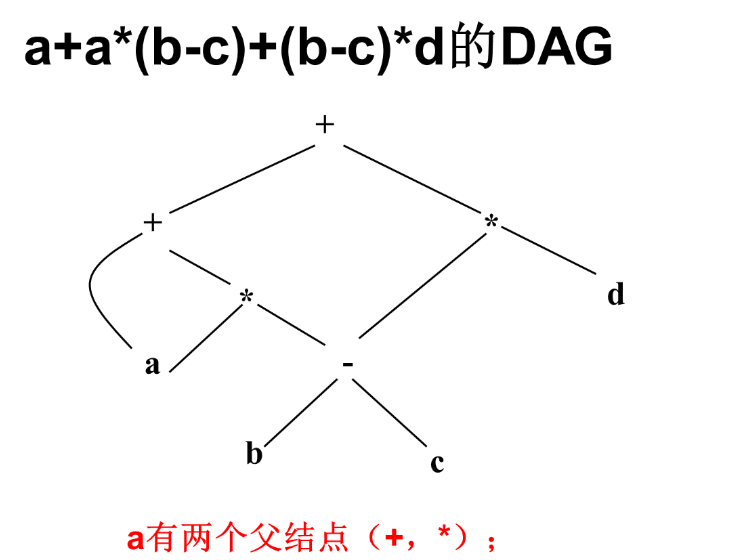
无循环有向图（Directed acyclic Graph，DAG）

例子：

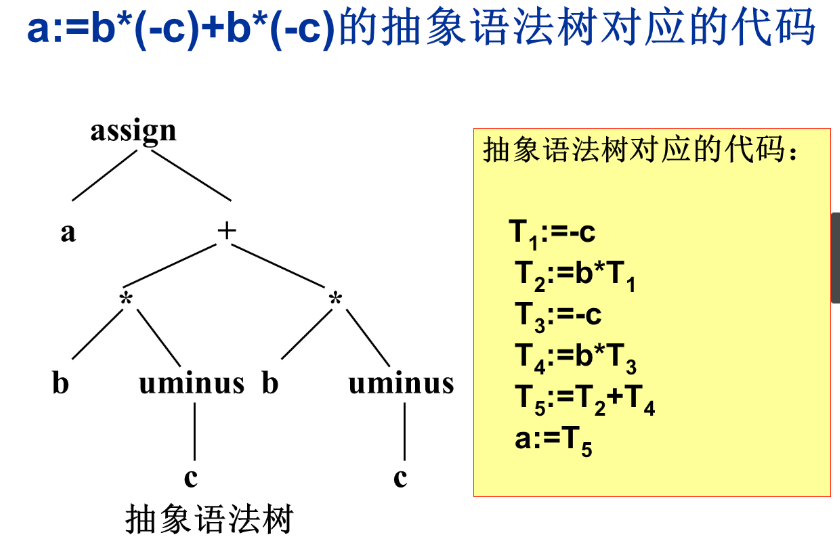
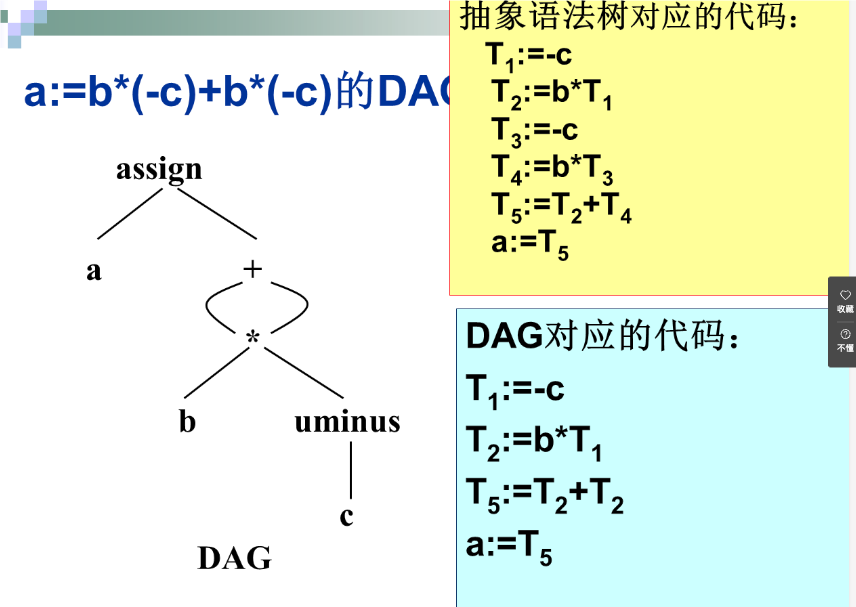
三地址代码

• 三地址代码 x：=y op z /每个语句的右边只能有一个运算符
• 三地址代码可以看成是抽象语法树或DAG的一种线性表示

例子：

###例子

j<,A,C,3
j, , ,13
j<,B,D,5
j, , ,13
j>,A,1,7
j, , ,10
+,y,z,T1
:=,T1, ,x
j, , ,12
-,y,z,T1
:=,T1, ,x
j, , ,1

一遍扫描实现的翻译模式

布尔表达式

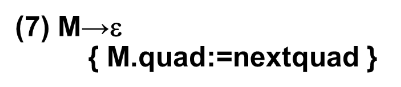
控制语句

第八章符号表

符号表的组织与作用

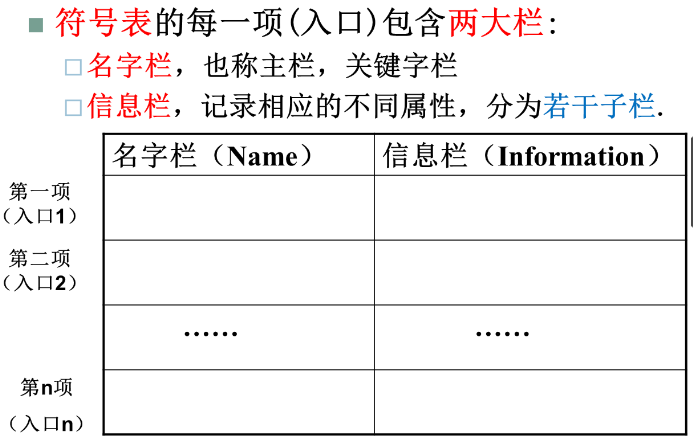
• 对符号表进行操作的时机

  • 定义出现：int x；
  • 使用性出现： if x<100

• 按照名字的不同种属建立多张符号表，如常数表，变量名表、过程名表

• 符号表的组织方式

  • 安排各项各栏的存储单元为固定长度

  • 用间接方式安排各栏存储单元

    

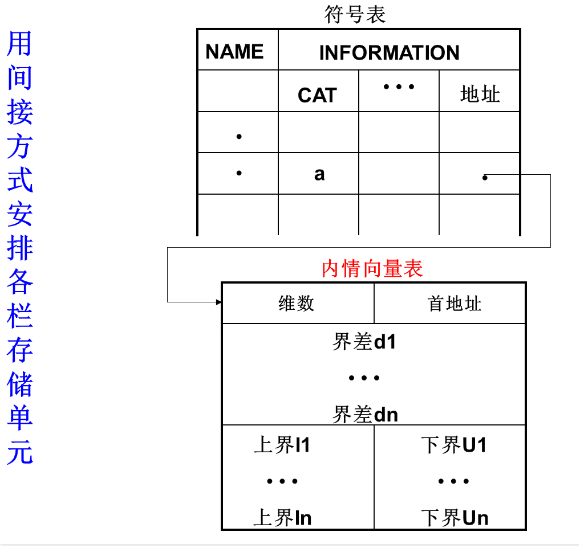
整理和查找

1. 线性查找
2. 二分查找
3. 杂凑查找（HASH技术）

名字的作用范围

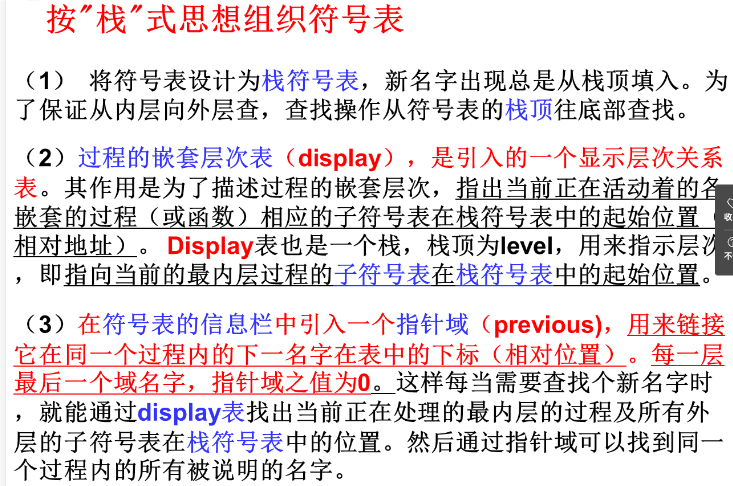
符号表的内容

第九章运行时存储空间组织

目标程序运行时的活动

运行时存储器的划分

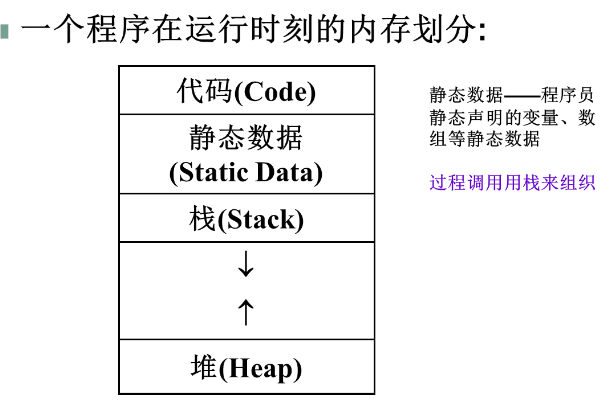
活动记录

存储分配策略

简单的栈式存储分配

嵌套过程语言的栈实现

第十章优化

概述

局部优化

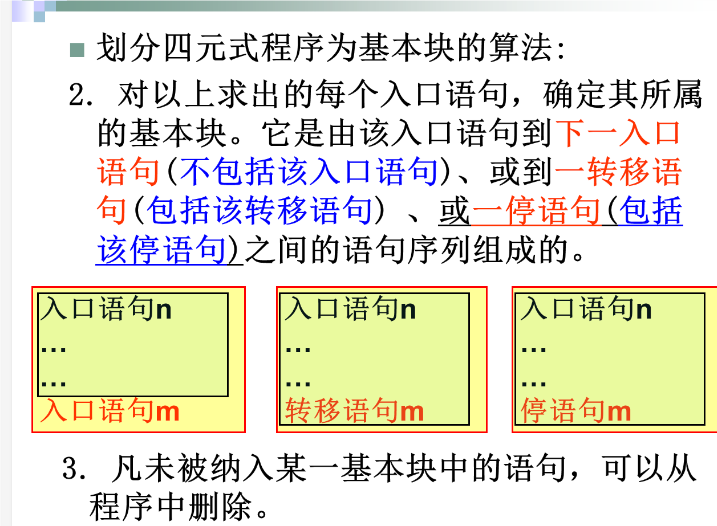
例子：