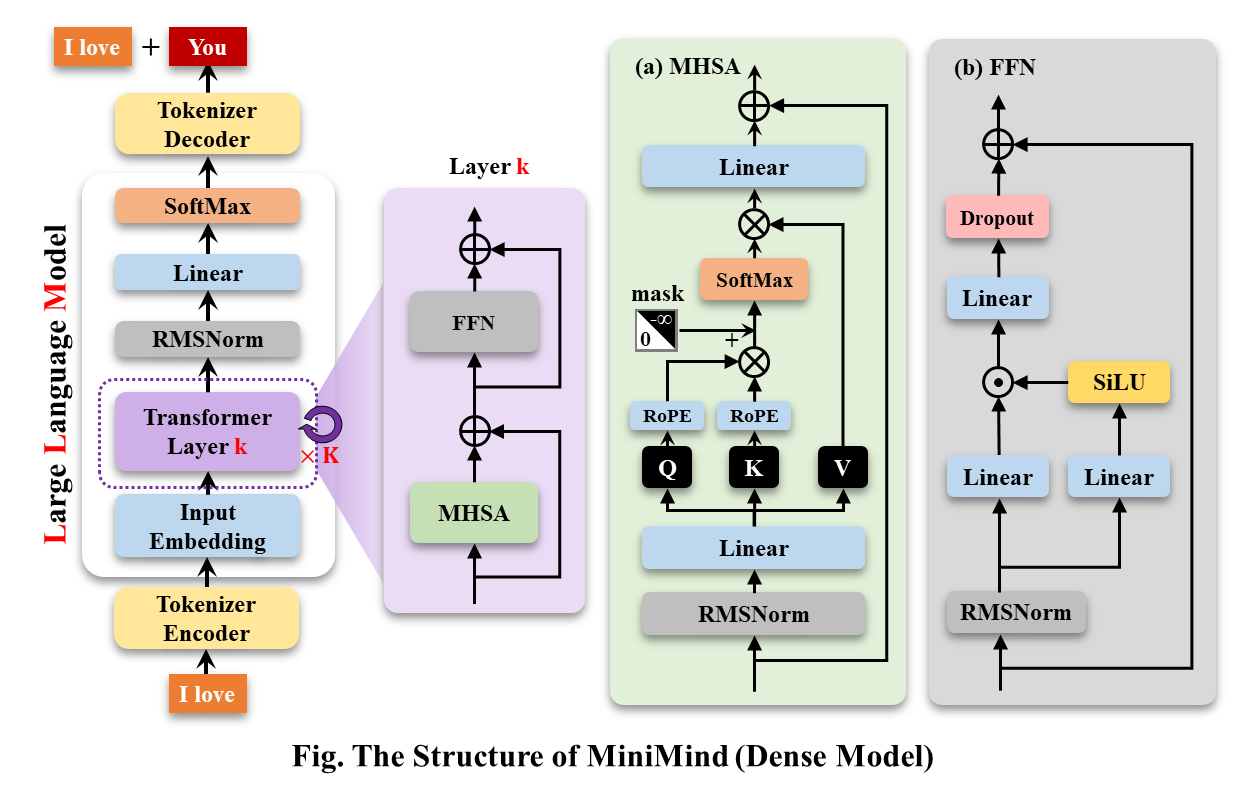
MiniMind训练记录

记录一下第一次训LLM，包括pretrain、SFT……，并把遇到的问题记录下来

SFT和instruction fine-tuing的关系？

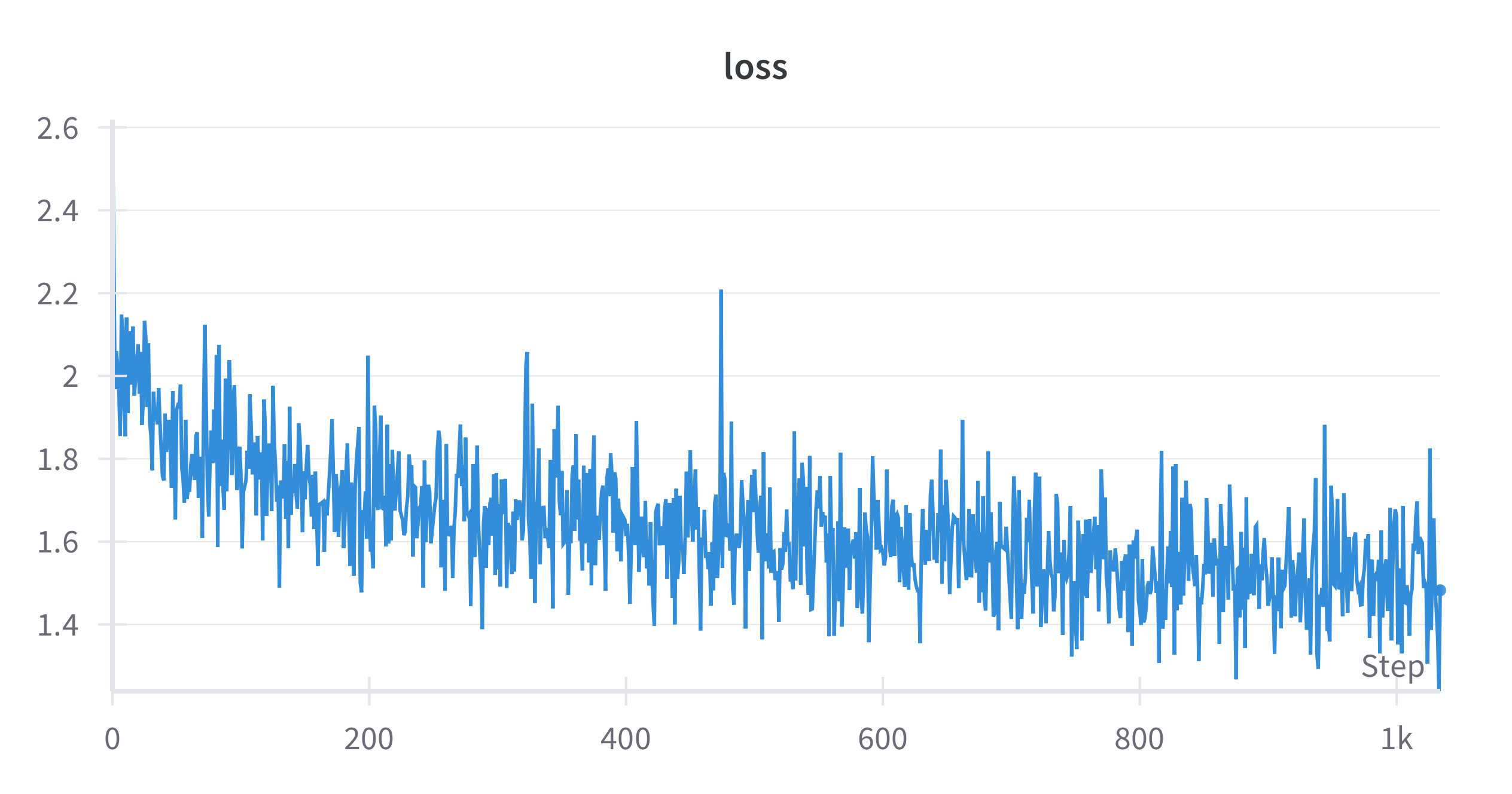
训练结果

Pre-Train

SFT

Tokenizer

算法：BPE
训练方式：无监督训练
训练流程：
1. 读取数据
2. 定义special token
3. 训练
4. 保存模型
数据：(unicode)

核心代码：

    # 初始化tokenizer  
    tokenizer = Tokenizer(models.BPE())  
    tokenizer.pre_tokenizer = pre_tokenizers.ByteLevel(add_prefix_space=False)  
 ​  
    # 定义特殊token  
    special_tokens = ["<unk>", "<s>", "</s>"]  
 ​  
    # 设置训练器并添加特殊token  
    trainer = trainers.BpeTrainer(  
        vocab_size=6400,  
        special_tokens=special_tokens,  # 确保这三个token被包含  
        show_progress=True,  
        initial_alphabet=pre_tokenizers.ByteLevel.alphabet()  
   )  
 ​  
    # 读取文本数据  
    texts = read_texts_from_jsonl(data_path)  
 ​  
    # 训练tokenizer  
    tokenizer.train_from_iterator(texts, trainer=trainer)  
 ​  
    # 设置解码器  
    tokenizer.decoder = decoders.ByteLevel()  
 ​  
    # 检查特殊token的索引  
    assert tokenizer.token_to_id("<unk>") == 0  
    assert tokenizer.token_to_id("<s>") == 1  
    assert tokenizer.token_to_id("</s>") == 2  
      
    # 保存tokenizer  
    tokenizer_dir = "./model/minimind_tokenizer"  
    os.makedirs(tokenizer_dir, exist_ok=True)  
    tokenizer.save(os.path.join(tokenizer_dir, "tokenizer.json"))  
    tokenizer.model.save("./model/minimind_tokenizer")

BEP算法的原理

字节对编码（Byte-Pair Encoding, BPE）是一种常用的分词算法，广泛用于自然语言处理任务中。BPE最初是一种数据压缩算法，但它在语言模型中被重新应用，特别是在处理不定长词汇的分词任务时具有很好的效果。BPE的主要思想是通过合并频率较高的字符对或词对，逐步构建词汇表，使得模型能够处理词汇中的不同词素或子词单元。以下是BPE算法的工作原理和步骤：

BPE算法的核心思想

BPE的核心思想是通过迭代地合并频率最高的字符或子词对，将文本分割成词根或子词单元，这样可以在一个较小的词汇表中实现更好的覆盖率，尤其在低频词或新词的处理上表现优异。这对于自然语言模型（如GPT、BERT）非常重要，因为这类模型往往需要一个有限的词汇表来处理大量的文本数据。

BPE算法的步骤

初始化：字符分解 将所有词汇分解成单独的字符。比如，”apple”会被分解成a p p l e。在这个初始阶段，每个字符都被视为一个独立的词素。
统计字符对频率 在分解后的词汇表中统计每一对连续字符的出现频率。例如，如果 “ap” 和 “pp” 在词汇表中出现频率最高，那么它们的频率就会被记录下来。
合并最高频率的字符对 找出频率最高的字符对，并将其合并成一个新的符号。例如，如果 “p p” 出现最多，则将其替换为一个新的子词 “pp”，使得 “apple” 变成 a pp l e。
更新词汇表 在整个词汇表中替换合并的字符对，同时更新词汇表，记录新的子词。然后，重复统计频率、合并字符对、更新词汇表的过程。
重复合并过程 上述过程会不断重复，直到词汇表的大小达到预先定义的上限或没有高频字符对可以合并。经过多次迭代，词汇表会逐渐从单字符组成的子词单元扩展为更长的词或词根单元。

BPE算法的优点

减少词汇表大小：通过将词汇分解成子词，BPE可以大幅缩减模型词汇表的大小，从而减少存储空间并提升计算效率。
处理未登录词：BPE的子词分解方式可以有效处理未登录词，即不在训练词汇表中的词。即便是全新词汇，也可以通过子词单元组合被模型理解。
通用性强：BPE适用于多种语言，在处理词形变化丰富的语言（如德语、芬兰语等）时尤其有效，因为其分解后的子词能涵盖词根、前缀和后缀等不同形式。

示例

假设我们有一个简单的词汇表，包含了以下词汇：low, lowest, newer, wider。通过BPE分词过程，这些词可以被逐步拆分和合并。例如：

初始状态下，所有词被拆解为单个字符：l o w, l o w e s t, n e w e r, w i d e r。
假设在此状态下，l o和w i出现频率较高，那么BPE会先将l o和w i合并。
经过多次合并，词汇表最终可能包括较长的子词，如low，wid和est等。

Pre-train

训练方式：无监督
数据：

训练过程：

  for step, (X, Y, loss_mask) in enumerate(train_loader):  
      X = X.to(args.device)  
      Y = Y.to(args.device)  
      loss_mask = loss_mask.to(args.device)  
 ​  
      lr = get_lr(epoch * iter_per_epoch + step, args.epochs * iter_per_epoch)  
      for param_group in optimizer.param_groups:  
          param_group["lr"] = lr  
 ​  
      with ctx:  
          out = model(X, Y)  
          loss = out.last_loss / args.accumulation_steps  
          loss_mask = loss_mask.view(-1)  
          loss = torch.sum(loss * loss_mask) / loss_mask.sum()  
 ​  
      scaler.scale(loss).backward()  
 ​  
      if (step + 1) % args.accumulation_steps == 0:  
          scaler.unscale_(optimizer)  
          torch.nn.utils.clip_grad_norm_(model.parameters(), args.grad_clip)  
 ​  
          scaler.step(optimizer)  
          scaler.update()  
​            optimizer.zero_grad(set_to_none=True)               

训练结果

Loss 计算

交叉熵损失：

交叉熵损失（Cross-Entropy Loss）是一种衡量两个概率分布之间差异的损失函数，常用于分类任务，尤其是多分类问题中。计算交叉熵损失时，我们通常将模型的输出概率分布与真实的类别标签分布进行比较，若两者的分布越接近，损失越小。

下面通过一个具体的例子来介绍交叉熵损失的计算过程。

交叉熵损失的公式

对于一个样本的交叉熵损失的计算公式为：

\[L = -\sum_{i=1}^{C} y_i \log(\hat{y}_i)\]

其中：

( C ) 是类别数。
( y_i ) 是实际的类别分布（通常是 one-hot 编码，只有一个位置为 1，其余为 0）。
$\hat{y}_i$ 是模型输出的预测概率（经过 softmax 层后得到的概率分布）。

在分类问题中，交叉熵损失会对每个样本计算一次，整个数据集的损失是所有样本的平均值。

示例

假设我们有一个分类任务，需要将样本分为三类 ( C = 3 )，类别分别为 0、1 和 2。

已知数据：

真实类别为类别 2（即标签为 ([0, 0, 1])）。
模型输出的概率分布为 $\hat{y} = [0.2, 0.3, 0.5]$。

计算过程：

表示实际分布 ( y )：真实类别是类别 2，因此我们用 one-hot 编码表示 ( y = [0, 0, 1] )。
预测概率分布 ( \hat{y} )：模型的预测概率为 (\hat{y} = [0.2, 0.3, 0.5])。
代入交叉熵公式： $L = -\sum_{i=1}^{C} y_i \log(\hat{y}_i)$

将真实标签 ( y = [0, 0, 1] ) 和预测概率 $hat{y} = [0.2, 0.3, 0.5]$ 代入，只有类别 2 的位置 $y_3 = 1$ 时才会有贡献，得到：
\[L = -[0 \cdot \log(0.2) + 0 \cdot \log(0.3) + 1 \cdot \log(0.5)]\]
简化为：
\[L = -\log(0.5)\]
计算交叉熵损失值：

$L = -\log(0.5) \approx 0.693$

解释

在这个例子中，交叉熵损失值为 ( 0.693 )。如果模型的预测概率分布与实际分布越接近（例如模型输出为 ([0, 0, 1])），则交叉熵损失值会更接近 0，表示模型的预测越准确。而如果模型输出偏离真实标签的概率（如 ([0.5, 0.3, 0.2])），交叉熵损失值将更高。

梯度累积

梯度累积是指在训练神经网络时，不是每次计算完损失后的反向传播都立即更新模型参数，而是累积多个小批量数据的梯度，再进行一次参数更新。这样做的主要目的是在显存有限的情况下，通过累积梯度来模拟更大的批量大小，从而稳定训练、提高模型性能。

在你的代码中：

 if (step + 1) % args.accumulation_steps == 0:  
    scaler.unscale_(optimizer)  
    torch.nn.utils.clip_grad_norm_(model.parameters(), args.grad_clip)  
    scaler.step(optimizer)  
    scaler.update()  
    optimizer.zero_grad(set_to_none=True)

这里的

args.accumulation_steps

就是设置的累积步数。代码的含义是：

梯度累积：在每次前向和反向传播后，梯度并没有被清零，而是累积起来。
条件判断：当达到设定的累积步数时（即 (step + 1) % args.accumulation_steps == 0），执行参数更新。
梯度剪裁：使用 clip_grad_norm_ 对梯度进行剪裁，防止梯度爆炸。
优化器更新：调用 scaler.step(optimizer)和 scaler.update()来更新参数。
清零梯度：使用 optimizer.zero_grad(set_to_none=True)将梯度清零，准备下一轮的累积。通过这种方式，可以在不增加显存占用的情况下，模拟更大的批量训练，有助于优化模型的收敛性和性能。

反放缩和裁剪?

SFT

（Full SFT Instruction fine tuning？）

指令微调

训练方式：有监督
数据：
训练过程：与pre-train 相同
核心代码: 与pre-train 相同
训练结果：

LORA

一些bug记录

deepspeed运行指定gpu

单节点全部卡：–master_port=25684 –num_gpus=4

单节点部分卡：–include localhost:1,2,3

注意：不能使用CUDA_VISIBLE_DEVICES，无论使用 CUDA_VISIBLE_DEVICES=1,2,3 bash，或者 CUDA_VISIBLE_DEVICES=1,2,3 deepspeed 都无效

例子：使用cuda:0 cuda:3 显卡，单机多卡运行 host:1,2,3