Why Can GPT ICL 论文粗读

💡 Meta Data

📜 研究背景 & 基础 & 目的 (Motivation)

LLM 涌现了few-shot In-Context learning的能力
- 通过少量示例可以预测训练的时候没有遇到的输入
但是ICL能力的机制还是个开放问题

🔬 研究方法

有人已经研究了发现：线性层的梯度下降和线性注意力形式上是类似的

工作一：解释ICL

transformer attention和梯度下降的形式非常类似，所以将语言模型解释为“元优化器”，将上下文学习理解为隐式微调：

公式推导：

q是当前推理到的token，X是前面不是示例的token，X‘是前面示例的token, $W_{ZSL}q$ 是 zero-shot下 q 的 attention 结果

初始公式

\[\begin{aligned}\mathcal{F}_{\mathrm{ICL}}(\mathbf{q})&=\mathrm{Attn}(V,K,\mathbf{q})\\&=W_V[X^{\prime};X]\operatorname{softmax}\left(\frac{(W_K[X^{\prime};X])^T\mathbf{q}}{\sqrt{d}}\right),\end{aligned}\]

2. 简化，线性化

\[\begin{aligned}\mathcal{F}_{\mathrm{ICL}}(\mathbf{q})&\approx W_V[X^{\prime};X]\left(W_K[X^{\prime};X]\right)^T\mathbf{q}\\&=W_VX\left(W_KX\right)^T\mathbf{q}+W_VX^{\prime}\left(W_KX^{\prime}\right)^T\mathbf{q}\\&\equiv\widetilde{\mathcal{F}}_{\mathrm{ICL}}(\mathbf{q}).\end{aligned}\]

3. 转换简化后的式子

\[\begin{aligned}\widetilde{\mathcal{F}}_{\mathrm{ICL}}(&(\mathbf{q})=W_\mathrm{ZSL}{\mathbf{q}}+W_VX^{\prime}\left(W_KX^{\prime}\right)^T\mathbf{q}\\&=W_\mathrm{ZSL}\mathbf{q}+\text{LinearAttn}\left(W_VX^{\prime},W_KX^{\prime},\mathbf{q}\right)\\&=W_{\mathrm{ZSL}}\mathbf{q}+\sum_iW_V\mathbf{x}_i^{\prime}\left(\left(W_K\mathbf{x}_i^{\prime}\right)^T\mathbf{q}\right)\\&=W_{\mathrm{ZSL}}\mathbf{q}+\sum_i\left((W_V\mathbf{x}_i^{\prime})\otimes(W_K\mathbf{x}_i^{\prime})\right)\mathbf{q}\\&=W_\mathrm{ZSL}{\mathbf{q}}+\Delta W_\mathrm{ICL}{\mathbf{q}}\\&=\left(W_{\mathrm{ZSL}}+\Delta W_{\mathrm{ICL}}\right)\mathbf{q}.\end{aligned}\]

所以ICL理解如下：

预训练的GPT充当元优化器
通过前向计算根据示范示例产生元梯度
然后通过注意力将这些元梯度应用于原始GPT，以构建ICL模型

ICL 与 fine-tuning 的关系 :

ICL 通过前向计算产生元梯度
微调通过反向传播计算梯度

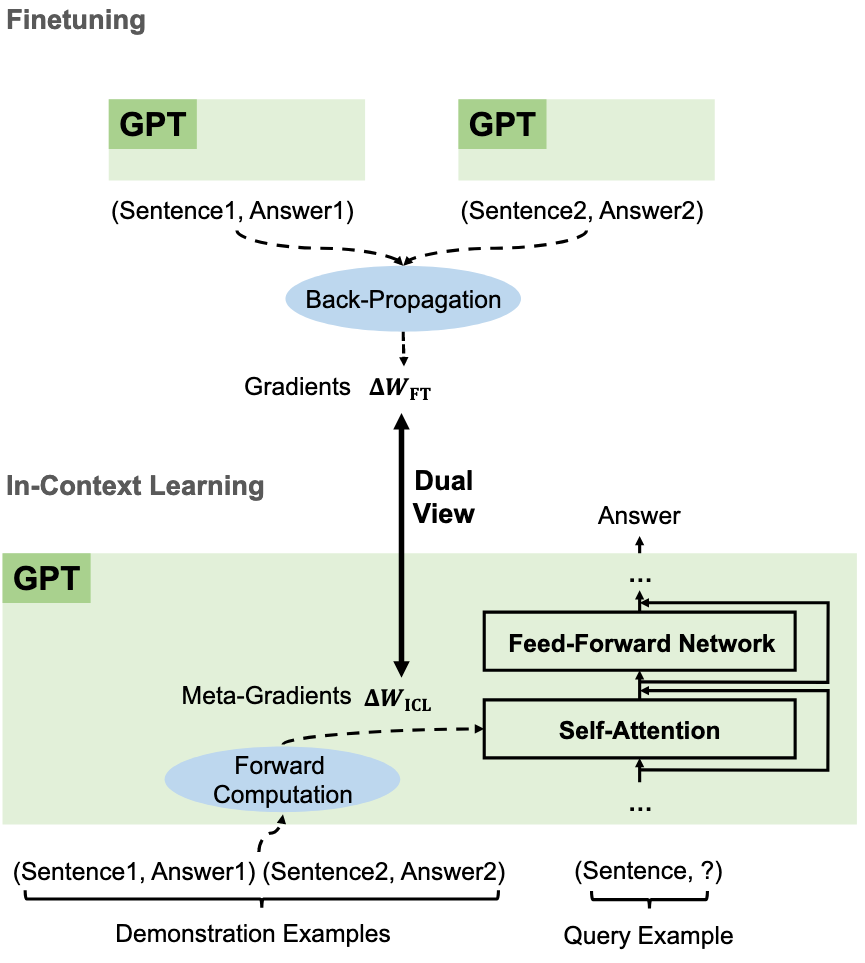
工作二：提出一种新的注意力机制

受到 fine-tuning 和 ICL 的相似性的启发，通过与基于动量的梯度下降类比设计了一种基于动量的注意力，比基础的注意力提升了性能。

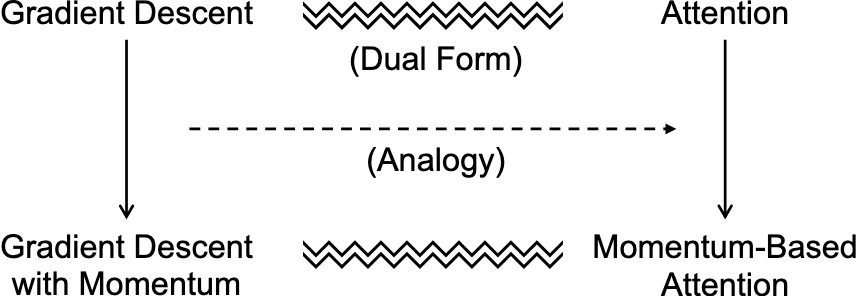
基于动量的梯度下降公式：

\[\Theta_t = \Theta_{t-1} - \gamma \sum_{i=1}^{t-1} \eta^{t-i} \nabla f_{\Theta_i}\]

参数更新时不仅考虑当前的梯度，还结合了过去多个时间步的梯度信息

基于动量的注意力机制公式：

\[\begin{aligned}\mathrm{MoAttn}(V,K,\mathbf{q}_t)&=\mathrm{Attn}(V,K,\mathbf{q}_t)+\mathrm{EMA}(V)\\&=V\mathrm{softmax}(\frac{K^{T}\mathbf{q}_{t}}{\sqrt{d}})+\sum_{i=1}^{t-1}\eta^{t-i}\mathbf{v}_{i},\end{aligned}\]